Control package
The control package is part of the Octave Forge project.
Function list[edit]
Linear System Representation[edit]
| Chapter | Function | Implemented | File |
|---|---|---|---|
| Basic Models | tf | yes | @tf/tf.m |
| zpk | yes | zpk.m | |
| ss | yes | @ss/ss.m | |
| frd | yes | @frd/frd.m | |
| pid | yes | pid.m | |
| pidstd | yes | pidstd.m | |
| pid2 | no | ||
| dss | yes | @lti/dss.m | |
| drss | no | ||
| filt | yes | filt.m | |
| rss | no | ||
| Tunable Models | ltiblock.gain | no | |
| ltiblock.pid | no | ||
| ltiblock.pid2 | no | ||
| ltiblock.ss | no | ||
| ltiblock.tf | no | ||
| realp | no | ||
| AnalysisPoint | no | ||
| genss | no | ||
| genfrd | no | ||
| genmat | no | ||
| getLoopTransfer | no | ||
| getIOTransfer | no | ||
| getSensitivity | no | ||
| getCompSensitivity | no | ||
| getPoints | no | ||
| replaceBlock | no | ||
| getValue | no | ||
| setValue | no | ||
| getBlockValue | no | ||
| setBlockValue | no | ||
| showBlockValue | no | ||
| showTunable | no | ||
| nblocks | no | ||
| getLFTModel | no | ||
| Model with Time Delays | pade | no | |
| absorbDelay | no | ||
| thiran | yes | thiran.m | |
| hasdelay | no | ||
| hasInternalDelay | no | ||
| totaldelay | no | ||
| delayss | no | ||
| setDelayModel | no | ||
| getDelayModel | no | ||
| Model Attributes | get | yes | @iddata/get.m |
| set | yes | @iddata/set.m | |
| tfdata | yes | @lti/tfdata.m | |
| zpkdata | yes | @lti/zpkdata.m | |
| ssdata | yes | @lti/ssdata.m | |
| frdata | yes | @lti/frdata.m | |
| piddata | no | ||
| pidstddata | no | ||
| piddata2 | no | ||
| pidstddata2 | no | ||
| dssdata | yes | @lti/dssdata.m | |
| chgFreqUnit | no | ||
| chgTimeUnit | no | ||
| isct | yes | @lti/isct.m | |
| isdt | yes | @lti/isdt.m | |
| isempty | yes | built-in function | |
| isfinite | yes | built-in function | |
| isParametric | no | ||
| isproper | no | ||
| isreal | yes | built-in function | |
| isiso | no | ||
| isstable | yes | @lti/isstable.m | |
| isstatic | no | ||
| order | no | ||
| ndims | yes | built-in function | |
| size | yes | built-in function | |
| Model Arrays | stack | no | |
| nmodels | no | ||
| permute | yes | built-in function | |
| reshape | yes | built-in function | |
| repsys | yes | repsys.m |
Model Interconnection[edit]
| Function | Implemented | File |
|---|---|---|
| feedback | yes | @lti/feedback.m |
| connect | yes | @lti/connect.m |
| sumblk | yes | sumblk.m |
| series | yes | @lti/series.m |
| parallel | yes | @lti/parallel.m |
| append | yes | append.m |
| blkdiag | yes | @lti/blkdiag.m |
| imp2exp | no | |
| inv | yes | built-in function |
| lft | no | |
| connectOptions | no |
Model Transformation[edit]
| Chapter | Function | Implemented | File | Number of Tests | Status | SLICOT functions | Priority (0-2) |
|---|---|---|---|---|---|---|---|
| Model Type Conversion | pidstd2 | no | |||||
| make1DOF | no | ||||||
| make2DOF | no | ||||||
| getComponents | no | ||||||
| Continuous-Discrete Conversion | c2d | yes | @lti/c2d.m | ||||
| d2c | yes | @lti/d2c.m | |||||
| d2d | yes | @lti/d2d.m | |||||
| upsample | no | ||||||
| c2dOptions | no | ||||||
| d2cOptions | no | ||||||
| d2dOptions | no | ||||||
| Model Simplification | hsvd | yes | hsvd.m | ||||
| hsvplot | no | ||||||
| sminreal | yes | @lti/sminreal.m | |||||
| balred | no | ||||||
| minreal | yes | @lti/minreal.m | |||||
| balreal | no | ||||||
| modred | no | ||||||
| balredOptions | no | ||||||
| hsvdOptions | no | ||||||
| State-Coordinate Transformation | canon | no | |||||
| prescale | yes | @lti/prescale.m | |||||
| ss2ss | no | ||||||
| xperm | yes | @lti/xperm.m | |||||
| Modal Decomposition | modsep | no | |||||
| stabsep | no | ||||||
| freqsep | no | ||||||
| stabsepOptions | no | ||||||
| freqsepOptions | no |
Linear Analysis[edit]
| Chapter | Function | Implemented | File | Number of Tests | Status | SLICOT functions | Priority (0-2) |
|---|---|---|---|---|---|---|---|
| Time-Domain Analysis | linearSystemAnalyzer | no | |||||
| impulseplot | no | ||||||
| initialplot | no | ||||||
| lsimplot | no | ||||||
| stepplot | no | ||||||
| covar | yes | covar.m | |||||
| impulse | yes | impulse.m | |||||
| initial | yes | initial.m | |||||
| lsim | yes | lsim.m | |||||
| step | yes | step.m | |||||
| lsiminfo | no | ||||||
| stepinfo | no | ||||||
| stepDataOptions | no | ||||||
| Frequency-Domain Analysis | bodeplot | no | |||||
| nicholsplot | no | ||||||
| nyquistplot | no | ||||||
| sigmaplot | no | ||||||
| bode | yes | bode.m | |||||
| nichols | yes | nichols.m | |||||
| nyquist | yes | nyquist.m | |||||
| sigma | yes | sigma.m | |||||
| evalfr | no | ||||||
| freqresp | yes | @lti/freqresp.m | |||||
| bandwidth | yes | built-in function | |||||
| dcgain | yes | @lti/dcgain.m | |||||
| getGainCrossover | no | ||||||
| getPeakGain | no | ||||||
| Stability Analysis | pole | yes | @lti/pole.m | ||||
| zero | yes | @lti/zero.m | |||||
| damp | yes | damp.m | |||||
| dsort | yes | dsort.m | |||||
| esort | yes | esort.m | |||||
| tzero | no | ||||||
| pzmap | yes | pzmap.m | |||||
| pzplot | no | ||||||
| iopzplot | no | ||||||
| allmargin | no | ||||||
| margin | yes | margin.m | |||||
| Plot Customization | bodeoptions | no | |||||
| hsvoptions | no | ||||||
| nicholsoptions | no | ||||||
| nyquistoptions | no | ||||||
| pzoptions | no | ||||||
| sigmaoptions | no | ||||||
| timeoptions | no | ||||||
| setoptions | no | ||||||
| getoptions | no | ||||||
| ctrlpref | no | ||||||
| updateSystem | no |
Control Design[edit]
| Chapter | Function | Implemented | File | Number of Tests | Status | SLICOT functions | Priority (0-2) |
|---|---|---|---|---|---|---|---|
| PID Controller Tuning | pidTuner | no | |||||
| pidtune | no | ||||||
| pidtuneOptions | no | ||||||
| SISO Feedback Loops | rlocus | yes | rlocus.m | ||||
| sgrid | no | ||||||
| rlocusplot | no | ||||||
| controlSystemDesigner | no | ||||||
| sisoinit | no | ||||||
| Linear-Quadratic-Gaussian Control | lqr | yes | lqr.m | ||||
| lqry | no | ||||||
| lqi | no | ||||||
| dlqr | yes | dlqr.m | |||||
| lqrd | no | ||||||
| kalman | yes | kalman.m | |||||
| kalmd | no | ||||||
| lqg | no | ||||||
| lqgreg | no | ||||||
| lqgtrack | no | ||||||
| augstate | no | ||||||
| norm | yes | @lti/norm.m | |||||
| Pole Placement | estim | yes | estim.m | ||||
| place | yes | place.m | |||||
| acker | yes | acker.m | |||||
| reg | no |
Matrix Computations[edit]
| Function | Implemented | File | Number of Tests | Status | SLICOT functions | Priority (0-2) |
|---|---|---|---|---|---|---|
| lyap | yes | lyap.m | ||||
| lyapchol | yes | lyapchol.m | ||||
| dlyap | yes | dlyap.m | ||||
| dlyapchol | yes | dlyapchol.m | ||||
| care | yes | care.m | ||||
| dare | yes | dare.m | ||||
| gcare | no | |||||
| gdare | no | |||||
| icare | no | |||||
| idare | no | |||||
| ctrb | yes | ctrb.m | ||||
| obsv | yes | obsv.m | ||||
| ctrbf | yes | ctrbf.m | ||||
| obsvf | yes | obsvf.m | ||||
| gram | yes | gram.m | ||||
| bdschur | no |
Examples[edit]
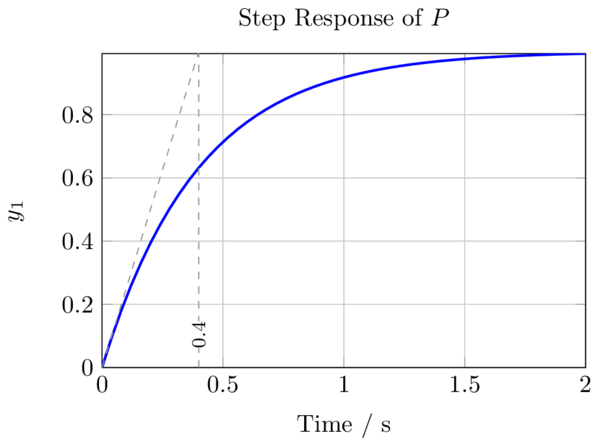
PT1 / Low-pass filter step response[edit]
| Code: Creating a transfer function and plotting its response |
T1 = 0.4; # time constant
P = tf([1], [T1 1]); # create transfer function model
step(P, 2) # plot step response
#add some common markers like the tangent line at the origin, which crosses lim(n->inf) f(t) at t=T1
hold on
plot ([0 T1], [0 1], "--", 'color', [.75 .75 .75])
plot ([T1 T1], [0 1], "--", 'color', [.75 .75 .75])
hold off
|
Bode Diagram with TikZ/PGFplots[edit]
We use the same system as before but we draw now with bode(P) a bode diagram.
The output is written to a .csv file.
| Code: Creating a transfer function and calculating its bode diagram |
T1 = 0.4; # time constant
P = tf([1], [T1 1]);
[mag, pha, w] = bode(P);
csvwrite("dat/bode_p.csv", [w', 20*log10(mag), pha]);
|
We can then invoke LaTeX with the following .tex file
| Code: Creating a bode diagram with pgfplots |
\documentclass[tikz]{standalone}
\usepackage{pgfplotstable}
\usepackage{siunitx}
\usetikzlibrary{pgfplots.groupplots}
\begin{document}
\pgfplotstableread[col sep=comma]{\detokenize{/path/to/csv/file/dat/bode_p.csv}}\datatable
\begin{tikzpicture}
\begin{groupplot}[
group style={rows=2},
width=0.8\textwidth,
height=0.4\textwidth,
xmajorgrids,
ymajorgrids,
enlarge x limits=false,
xmode=log,
]
\nextgroupplot[
title={Bode Diagram of $P$},
ylabel={Magnitude / \si{\decibel}},
]
\addplot[blue,line width=1pt] table[x index=0,y index=1]{\datatable};
\nextgroupplot[
xlabel={Frequency / \si{\radian\per\second}},
ylabel={Phase / \si{\degree}},
]
\addplot[red,line width=1pt] table[x index=0,y index=2]{\datatable};
\end{groupplot}
\end{tikzpicture}
\end{document}
|
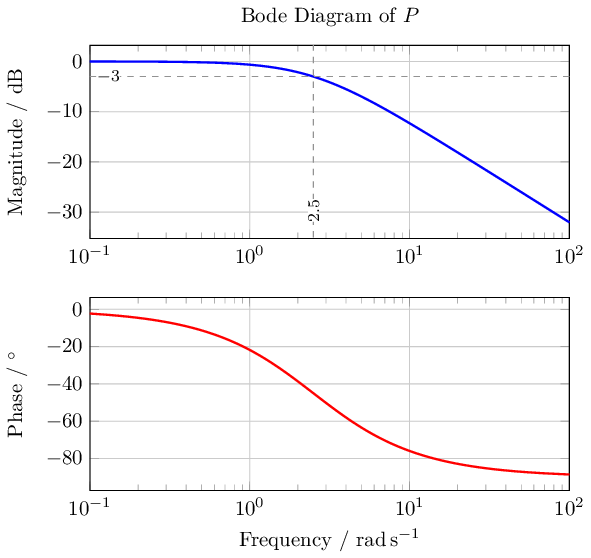
to generate a beautiful bode diagram
It can be seen that a first order low-pass filter has magnitude at .
Inverted Pendulum[edit]
Model[edit]
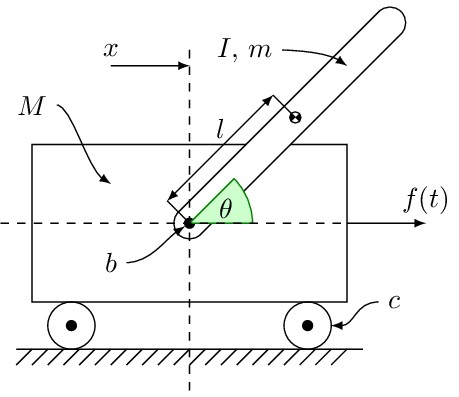
A nonlinear model of the inverted pendulum can be derived by
where the variables are defined as
| Name | Definition |
|---|---|
| Mass of the cart | |
| Mass of the pendulum | |
| Translational damping coefficient | |
| Length of the pendulum | |
| Inertia of the pendulum | |
| Rotational damping coefficient |
Linearization around the point and substitution of (from here on in the analysis, will be written as , but it should be noted that now measures from a new reference) leads to
This can be expressed in the frequency domain like
Transfer functions[edit]
By dividing the state variables by the input one obtains the transfer functions
with
This can be expressed in Octave
| Code: Creating the transfer functions for the inverted pendulum |
m = 0.15;
l = 0.314;
M = 1.3;
I = 0;
g = 9.80665;
b = 20;
c = 20;
G1 = tf([m*l^2+I b -m*g*l],
[(M+m)*(m*l^2+I)-m^2*l^2 (M+m)*b+(m*l^2+I)*c -(M+m)*m*g*l+b*c -m*g*l*c 0]);
G2 = tf([-m*l],
[(M+m)*(m*l^2+I)-m^2*l^2 (M+m)*b+(m*l^2+I)*c -(M+m)*m*g*l+b*c -m*g*l*c]);
|
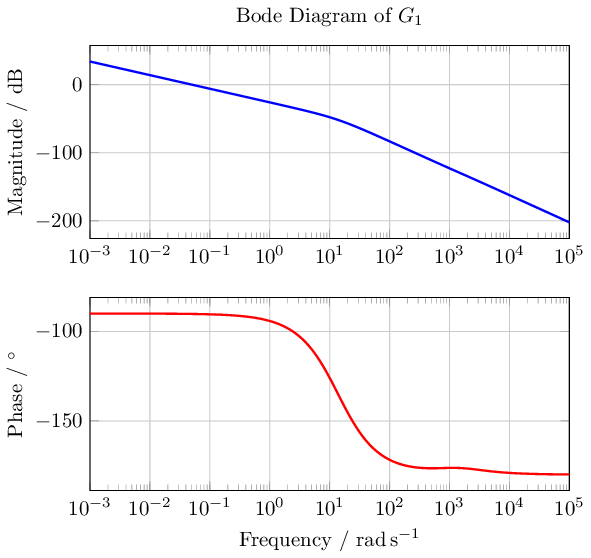
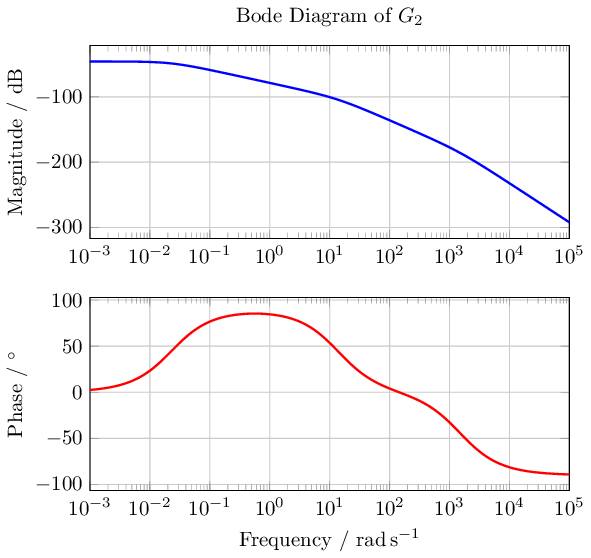
and by invoking the bode command
| Code: Creating Bode plots for the inverted pendulum |
bode(G1);
bode(G2);
|
one obtains the bode diagrams of the two transfer functions.