User:Hg200: Difference between revisions
(Created page with "= Investigations on update_camera() = In the second part of <math display="inline">\rightarrow</math> axes::properties::update_camera () the view transformation "x_gl_mat1" a...") |
No edit summary |
||
| Line 25: | Line 25: | ||
// Construct a 4x4 matrix "x_view" that is a subset of "x_gl_mat1" | // Construct a 4x4 matrix "x_view" that is a subset of "x_gl_mat1" | ||
// Start with identity I = [1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1] | |||
Matrix x_view = xform_matrix (); | Matrix x_view = xform_matrix (); | ||
// #7 -> #8 | // Step #7 -> #8 | ||
scale (x_view, 1, 1, -1); | scale (x_view, 1, 1, -1); | ||
Matrix l = xform_matrix (); | Matrix l = xform_matrix (); | ||
| Line 32: | Line 33: | ||
l(1,0) = u(0); l(1,1) = u(1); l(1,2) = u(2); | l(1,0) = u(0); l(1,1) = u(1); l(1,2) = u(2); | ||
l(2,0) = -f(0); l(2,1) = -f(1); l(2,2) = -f(2); | l(2,0) = -f(0); l(2,1) = -f(1); l(2,2) = -f(2); | ||
// #6 -> #7 (rotate on the Z axis) | // Step #6 -> #7 (rotate on the Z axis) | ||
x_view = x_view * l; | x_view = x_view * l; | ||
// #5 -> #6 | // Step #5 -> #6 | ||
translate (x_view, -c_eye(0), -c_eye(1), -c_eye(2)); | translate (x_view, -c_eye(0), -c_eye(1), -c_eye(2)); | ||
// #4 -> #5 | // Step #4 -> #5 | ||
scale (x_view, pb(0), pb(1), pb(2)); | scale (x_view, pb(0), pb(1), pb(2)); | ||
// #3 -> #4 | // Step #3 -> #4 | ||
translate (x_view, -0.5, -0.5, -0.5); | translate (x_view, -0.5, -0.5, -0.5); | ||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
Revision as of 11:05, 20 September 2020
Investigations on update_camera()
In the second part of axes::properties::update_camera () the view transformation "x_gl_mat1" and projection matrix "x_gl_mat2" are put together. The following images illustrate some of the properties of "x_gl_mat1".
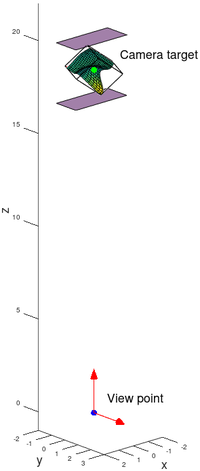
The Octave coordinate system
In Octave a plot scene is defined by a "view point", a "camera target" and an "up vector".
The role of "x_gl_mat1"
The following section of code assembles the matrix "x_view", which is a subset of "x_gl_mat1". The matrix "x_gl_mat1" consists of different translations, scalings and a rotation operation.
| Code: Section of axes::properties::update_camera ()" |
// Unit length vectors for direction of view "f" and up vector "UP"
ColumnVector F (c_center), f (F), UP (c_upv);
normalize (f);
normalize (UP);
// Calculate the vector rejection UP onto f
// s, f and u are used to assemble the rotation matrix l
ColumnVector s = cross (f, UP);
ColumnVector u = cross (s, f);
// Construct a 4x4 matrix "x_view" that is a subset of "x_gl_mat1"
// Start with identity I = [1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1]
Matrix x_view = xform_matrix ();
// Step #7 -> #8
scale (x_view, 1, 1, -1);
Matrix l = xform_matrix ();
l(0,0) = s(0); l(0,1) = s(1); l(0,2) = s(2);
l(1,0) = u(0); l(1,1) = u(1); l(1,2) = u(2);
l(2,0) = -f(0); l(2,1) = -f(1); l(2,2) = -f(2);
// Step #6 -> #7 (rotate on the Z axis)
x_view = x_view * l;
// Step #5 -> #6
translate (x_view, -c_eye(0), -c_eye(1), -c_eye(2));
// Step #4 -> #5
scale (x_view, pb(0), pb(1), pb(2));
// Step #3 -> #4
translate (x_view, -0.5, -0.5, -0.5);
|
To visualize the matrix properties, the "x_gl_mat1" matrix is multiplied by the object coordinates. The plot box is now aligned with the Z-axis and the view point is at the origin . The matrix transforms world coordinates into camera coordinates. The purple planes show the near and far clipping planes.
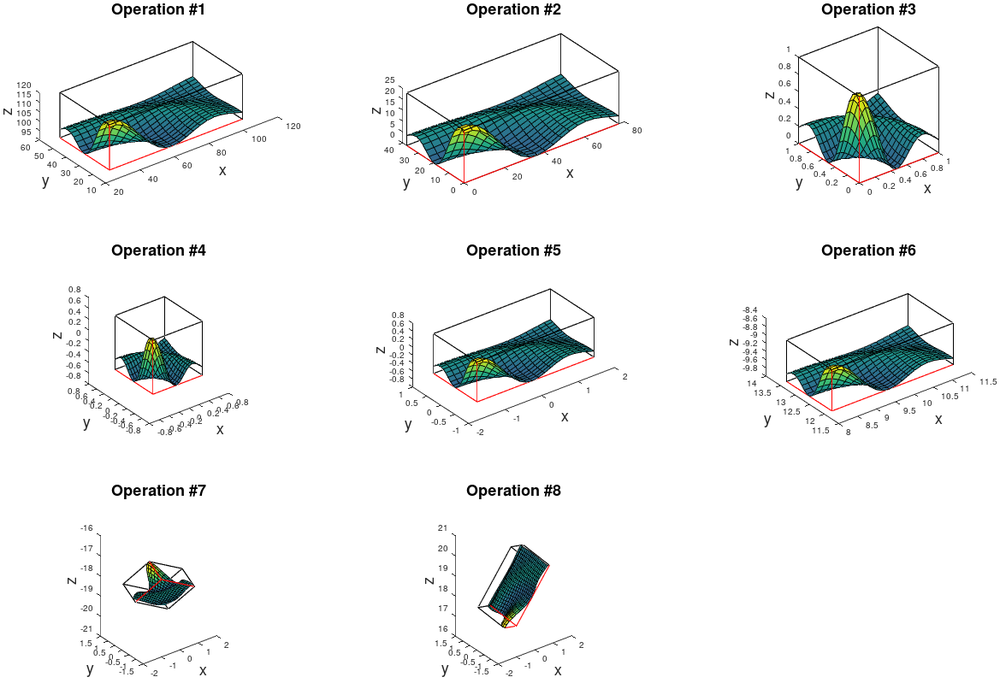
The individual translation, scaling and rotation operations of "x_gl_mat1", are shown in the following figure:

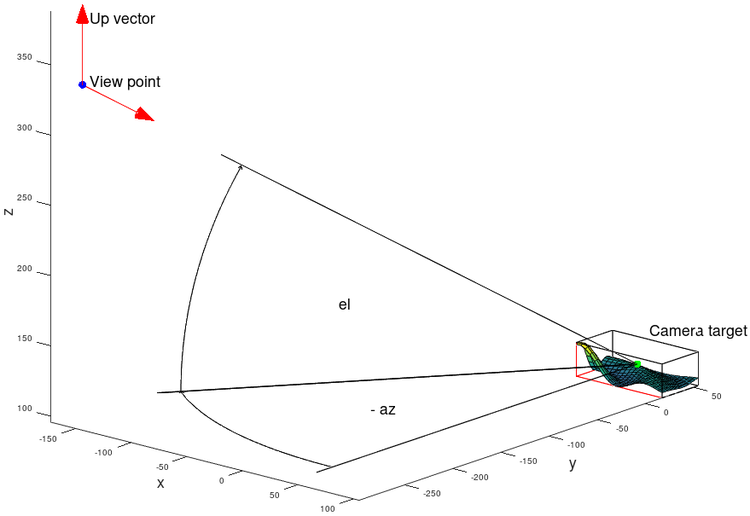
![{\textstyle [0,0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ced759f6efbc47419d3fda1d17d8dfbeeb822b85)