User:Hg200

Investigations on update_camera()

In the second part of ${\textstyle \rightarrow }$ "axes::properties::update_camera ()" the view transformation "x_gl_mat1" and projection matrix "x_gl_mat2" are put together. The following article illustrates some of the properties of "x_gl_mat1" and "x_gl_mat2".

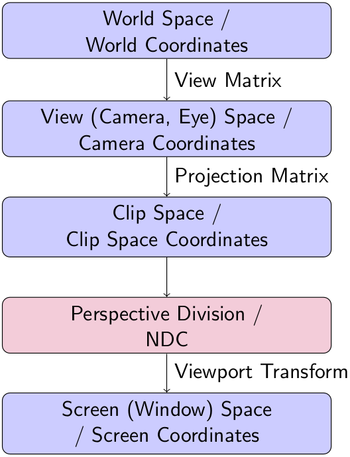
OpenGL coordinate systems

In the Octave plotting backend, we find various OpenGL transformations. Some of the classic OpenGL transformation steps, as well as coordinate systems, are shown in the following picture:

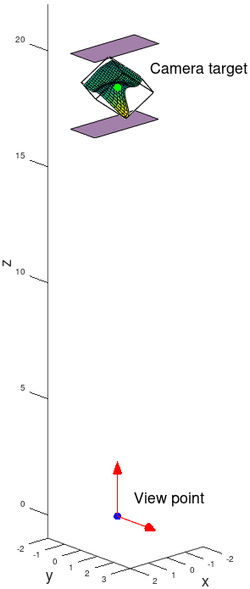
The Octave coordinate system

In Octave a plot scene is defined by a "view point", a "camera target" and an "up vector".

The role of "x_gl_mat1"

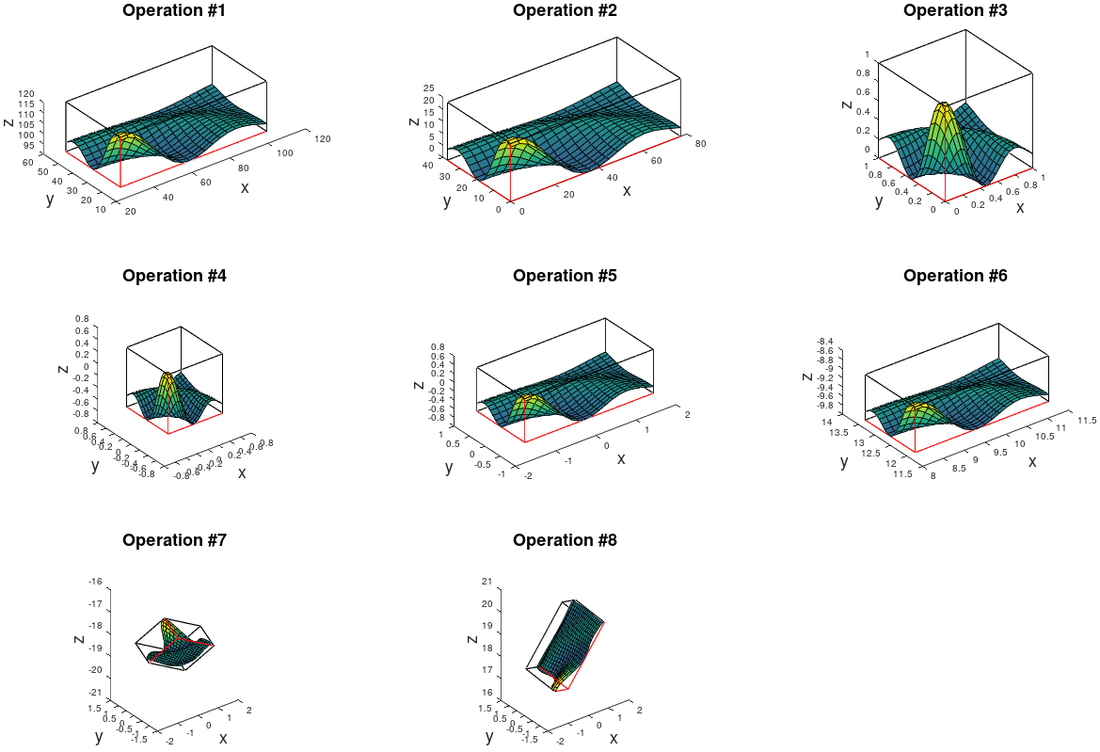
The following section of code composes the matrix "x_view", which is a subset of "x_gl_mat1". The matrix "x_gl_mat1" consists of multiple translations, scales and one rotation operation.

Code: Section of axes::properties::update_camera ()"

// Unit length vector for direction of view "f" and up vector "UP" ColumnVector F (c_center), f (F), UP (c_upv); normalize (f); normalize (UP); // Scale "UP" vector, so that norm(f x UP) becomes 1 if (std::abs (dot (f, UP)) > 1e-15) { double fa = 1 / sqrt (1 - f(2)*f(2)); scale (UP, fa, fa, fa); } // Calculate the vector rejection UP onto f // s, f and u are used to assemble the rotation matrix l ColumnVector s = cross (f, UP); ColumnVector u = cross (s, f); // Construct a 4x4 matrix "x_view" that is a subset of "x_gl_mat1" // Start with identity I = [1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1] Matrix x_view = xform_matrix (); // Step #7 -> #8 scale (x_view, 1, 1, -1); Matrix l = xform_matrix (); l(0,0) = s(0); l(0,1) = s(1); l(0,2) = s(2); l(1,0) = u(0); l(1,1) = u(1); l(1,2) = u(2); l(2,0) = -f(0); l(2,1) = -f(1); l(2,2) = -f(2); // Step #6 -> #7 (rotate on the Z axis) x_view = x_view * l; // Step #5 -> #6 translate (x_view, -c_eye(0), -c_eye(1), -c_eye(2)); // Step #4 -> #5 scale (x_view, pb(0), pb(1), pb(2)); // Step #3 -> #4 translate (x_view, -0.5, -0.5, -0.5);

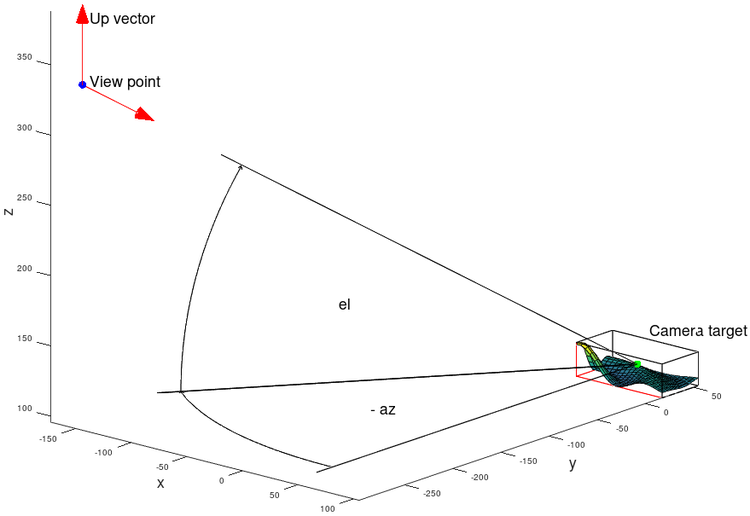
To visualize the matrix properties, the "x_gl_mat1" matrix is multiplied by the object coordinates. The plot box is now aligned with the Z-axis and the view point is at the origin ${\textstyle [0,0,0]}$. The matrix transforms world coordinates into camera coordinates. The purple planes show the near and far clipping planes.

The individual translation, scaling and rotation operations of "x_gl_mat1", are shown in the following figure:

The role of "x_gl_mat2"

The matrix "x_gl_mat2" is composed of the sub matrices "x_viewport" and "x_projection". The purpose of these matrices is to fit the 2D image of the above transformation result into a "bounding box". The bounding box is defined as follows:

 bb(0), bb(1): Position of the "viewport"
 bb(2), bb(3): Width and height of the "viewport"

Hint: If you debug in "update_camera ()", you can print "bb":

 (gdb) print *bb.rep.data@bb.rep.len

Compare the result with the output in the Octave prompt:

 hax = axes ();
 get (hax, "position");

In the following simplified code section, the field of view (FOV) is determined such that the image is fitted into the bounding box of the window:

Code: Section of axes::properties::update_camera ()"

if (cameraviewanglemode_is ("auto")) { if ((bb(2)/bb(3)) > (xM/yM)) // When the image is scaled to the size of the bounding box, // the height collides with the bounding box first. Therefore, // the camera view angle is defined by the image height yM. af = 1.0 / yM; else // The image width collides with the bounding box. af = 1.0 / xM; // The view angle "v_angle", also called field of view "FOV", // is formed by the hypotenuse and the adjacent side, which is given by // the distance between the view point and the camera target "norm (F)". // The ratio of the opposite side, given by "af", to the adjacent side in // a right-angled triangle is the tangent of the view angle. v_angle = 2 * (180.0 / M_PI) * atan (1 / (2 * af * norm (F))); cameraviewangle = v_angle; } else v_angle = get_cameraviewangle (); // Calculate backwards from the angle to the ratio. This step // is necessary because "v_angle" can be set manually. double pf = 1 / (2 * tan ((v_angle / 2) * M_PI / 180.0) * norm (F)); // Normalize to one. Resulting coordinates are "normalized device coordinates". scale (x_projection, pf, pf, 1);

"x_viewport" is a 2D transformation used to place the "normalized" plot box in the center of the bounding box:

Code: Section of axes::properties::update_camera ()"

double pix = 1; if (autocam) { if ((bb(2)/bb(3)) > (xM/yM)) pix = bb(3); else pix = bb(2); } else pix = (bb(2) < bb(3) ? bb(2) : bb(3)); // Move to the center of the bounding box inside the figure. translate (x_viewport, bb(0)+bb(2)/2, bb(1)+bb(3)/2, 0); // Scale either to width or height, to fit correctly into the bounding box scale (x_viewport, pix, -pix, 1); x_gl_mat2 = x_viewport * x_projection;

Note: The projection matrix just scales x, y so that the image fits tightly into the bounding box. The z-coordinate is not modified!