User:Hg200

Investigations on update_camera()

In the second part of ${\textstyle \rightarrow }$ axes::properties::update_camera () the view transformation "x_gl_mat1" and projection matrix "x_gl_mat2" are put together. The following images illustrate some of the properties of "x_gl_mat1".

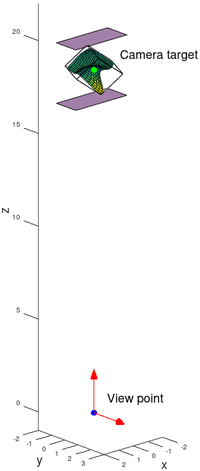
The Octave coordinate system

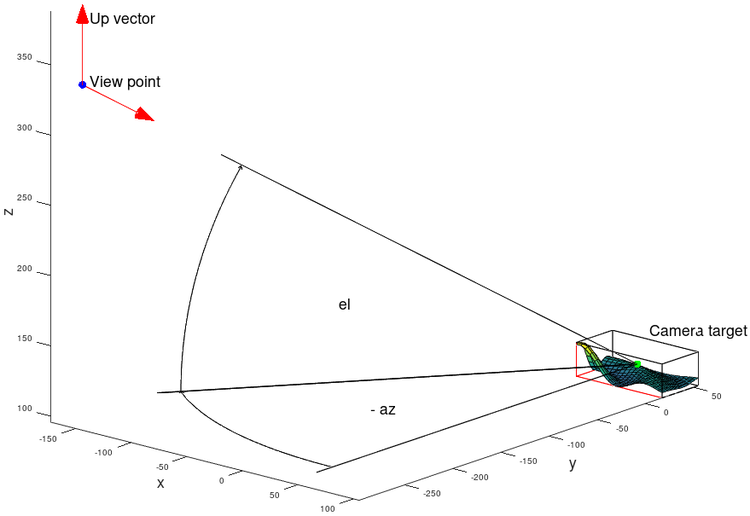
In Octave a plot scene is defined by a "view point", a "camera target" and an "up vector".

The role of "x_gl_mat1"

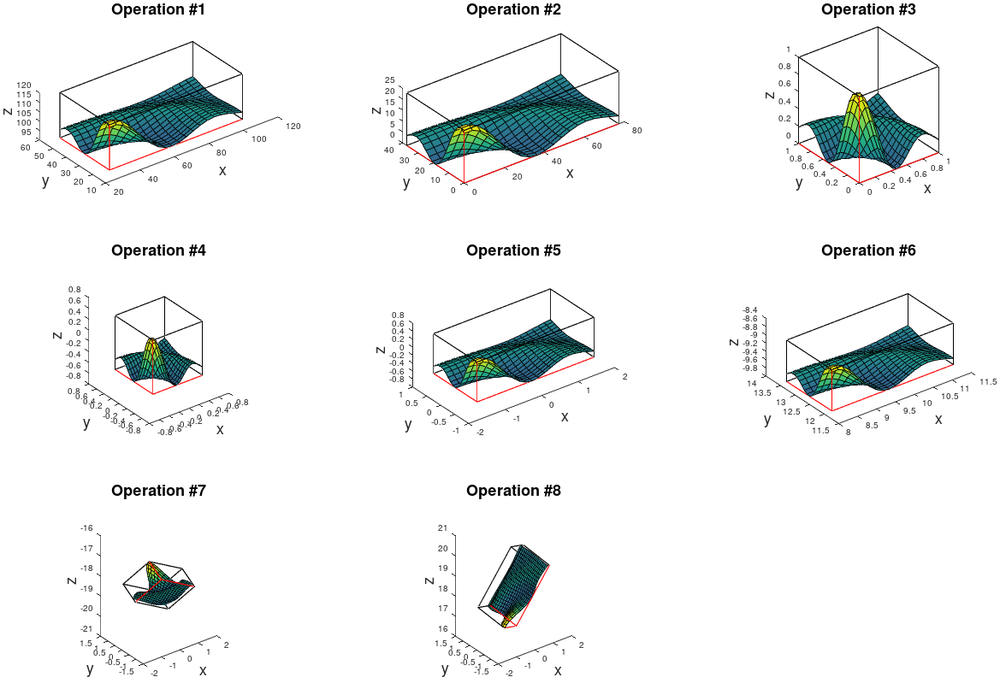
The following section of code assembles the matrix "x_view", which is a subset of "x_gl_mat1". The matrix "x_gl_mat1" consists of different translations, scalings and a rotation operation.

Code: Section of axes::properties::update_camera ()"

// Unit length vectors for direction of view "f" and up vector "UP" ColumnVector F (c_center), f (F), UP (c_upv); normalize (f); normalize (UP); // Calculate the vector rejection UP onto f // s, f and u are used to assemble the rotation matrix l ColumnVector s = cross (f, UP); ColumnVector u = cross (s, f); // Construct a 4x4 matrix "x_view" that is a subset of "x_gl_mat1" Matrix x_view = xform_matrix (); // #7 -> #8 scale (x_view, 1, 1, -1); Matrix l = xform_matrix (); l(0,0) = s(0); l(0,1) = s(1); l(0,2) = s(2); l(1,0) = u(0); l(1,1) = u(1); l(1,2) = u(2); l(2,0) = -f(0); l(2,1) = -f(1); l(2,2) = -f(2); // #6 -> #7 (rotate on the Z axis) x_view = x_view * l; // #5 -> #6 translate (x_view, -c_eye(0), -c_eye(1), -c_eye(2)); // #4 -> #5 scale (x_view, pb(0), pb(1), pb(2)); // #3 -> #4 translate (x_view, -0.5, -0.5, -0.5);

To visualize the matrix properties, the "x_gl_mat1" matrix is multiplied by the object coordinates. The plot box is now aligned with the Z-axis and the view point is at the origin ${\textstyle [0,0,0]}$. The matrix transforms world coordinates into camera coordinates. The purple planes show the near and far clipping planes.

The individual translation, scaling and rotation operations of "x_gl_mat1", are shown in the following figure: