TISEAN package: Difference between revisions
m (Rename "Octave-Forge" to "Octave Forge" (https://lists.gnu.org/archive/html/octave-maintainers/2018-08/msg00138.html).) |
|||
| (47 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
= Porting TISEAN = | == Porting TISEAN == | ||
This | This section which focuses on demonstrating how the package is to be ported and what is the current state of that process is located in [[TISEAN_package:Procedure]]. | ||
== Tutorials == | |||
These tutorials are based on examples, tutorials and the articles located on the TISEAN website:<br/> [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/ http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/].<br/> | |||
This tutorial will utilize the following dataset: | |||
* [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/tutorial/amplitude.dat amplitude.dat] | |||
Please download it as the tutorial will reference it. | |||
=== False Nearest Neighbors === | |||
This function uses a method to determine the minimum sufficient embedding dimension. It is based on the [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node9.html#SECTION00032200000000000000 False Nearest Neighbors] section of the TISEAN documentation. As a demonstration we will create a plot that contains an Ikeda Map, a Henon Map and a Henon Map corrupted by 10% of Gaussian noise. | |||
{{Code|Analyzing false nearest neighbors|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create maps | |||
ikd = ikeda (10000); | |||
hen = henon (10000); | |||
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3)); | |||
# Create and plot false nearest neighbors | |||
[dim_ikd, frac_ikd] = false_nearest (ikd(:,1)); | |||
[dim_hen, frac_hen] = false_nearest (hen(:,1)); | |||
[dim_hen_noisy, frac_hen_noisy] = false_nearest (hen_noisy(:,1)); | |||
plot (dim_ikd, frac_ikd, '-b*;Ikeda;',... | |||
dim_hen, frac_hen, '-r+;Henon;',... | |||
dim_hen_noisy, frac_hen_noisy, '-gx;Henon Noisy;'); | |||
</syntaxhighlight>}} | |||
The {{Codeline|dim_*}} variables hold the dimension (so here 1:5), and {{Codeline|frac_*}} contain the fraction of false nearest neighbors. From this chart we can obtain the sufficient embedding dimension for each system. For a Henon Map {{Codeline|m = 2}} is sufficient, but for an Ikeda map it is better to use {{Codeline|m = 3}}. | |||
[[File:tisean_false_neigh.png|400px|center]] | |||
The | === Finding Unstable Periodic Orbits === | ||
Here I will demonstrate how to find unstable periodic orbits. This section is based on the TISEAN documentation chapter [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node19.html#SECTION00053000000000000000 Finding unstable periodic orbits]. We will start by finding these orbits using function {{Codeline|upo}}. | |||
{{Code|Finding unstable periodic orbits|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create maps | |||
hen = henon (1000); | |||
hen = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3)); | |||
# Find orbits | |||
[lengths, data] = upo(hen(:,1), 2, 'p',6,'v',0.1, 'n', 100); | |||
</syntaxhighlight>}} | |||
The vector {{Codeline|lengths}} contains the size of each of the found orbits and {{Codeline|data}} contains their coordinates. To obtain delay coordinates and plot these orbits onto the original data we will use {{Codeline|upoembed}}. | |||
{{Code|Plotting unstable periodic orbits|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create delay coordinates for the orbits and data | |||
up = upoembed (lengths, data, 1); | |||
delay_hen = delay (hen(:,1)); | |||
# Plot all of the data | |||
plot (delay_hen(:,1), delay_hen(:,2), 'r.;Noisy Henon;','markersize',2,... | |||
up{4}(:,1), up{4}(:,2),'gx;Fixed Point;','markersize',20,'linewidth',1, ... | |||
up{3}(:,1), up{3}(:,2),'b+;Period 2;','markersize',20,'linewidth',1, ... | |||
up{2}(:,1), up{2}(:,2),'ms;Period 6;','markersize',20,'linewidth',1, ... | |||
up{1}(:,1), up{1}(:,2),'cs;Period 6;','markersize',20,'linewidth',1); | |||
</syntaxhighlight>}} | |||
[[File:Upo.png|400px|center]] | |||
The plotting options are passed to make the orbits more visible. | |||
[[File: | === Nonlinear Prediction === | ||
In this section we will demonstrate some functions from the 'Nonlinear Prediction' chapter of the TISEAN documentation (located [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node16.html#SECTION00050000000000000000 here]). For now this section will only demonstrate functions that are connected to the [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node18.html#SECTION00052000000000000000 Simple Nonlinear Prediction] section. <br/> | |||
There are three functions in this section: {{Codeline|lzo_test}}, {{Codeline|lzo_gm}} and {{Codeline|lzo_run}}. The first is used to estimate the forecast error for a set of chosen parameters, the second gives some global information about the fit and the third produces predicted points. Let us start with the first one (before starting this example remember to download 'amplitude.dat' from above and start Octave in the directory that contains it). The pairs of parameters {{Codeline|(m,d)}} where chosen after the TISEAN documentation. | |||
{{Code|Analyzing forecast errors for various parameters|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Load data | |||
load amplitude.dat | |||
# Create different forecast error results | |||
steps = 200; | |||
res1 = lzo_test (amplitude(1:end-200), 'm', 2, 'd', 6, 's', steps); | |||
res2 = lzo_test (amplitude(1:end-200), 'm', 3, 'd', 6, 's', steps); | |||
res3 = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 1, 's', steps); | |||
res4 = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps); | |||
plot (res1(:,1), res1(:,2), 'r;m = 2, d = 6;', ... | |||
res2(:,1), res2(:,2), 'g;m = 3, d = 6;',... | |||
res3(:,1), res3(:,2), 'b;m = 4, d = 1;',... | |||
res4(:,1), res4(:,2), 'm;m = 4, d = 6;'); | |||
</syntaxhighlight>}} | |||
[[File:tisean_nl_prediction.png|400px|center]] | |||
It seems that the last pair {{Codeline|(m = 4, d = 6)}} is suitable. We will use it to determine the the best neighborhood to use when generating future points. | |||
{{Code|Determining the best neighborhood size using lzo_gm|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
gm = lzo_gm (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps, 'rhigh', 20); | |||
</syntaxhighlight>}} | |||
After analyzing {{Codeline|gm}} it is easy to observe that the least error is for the first neighborhood size of {{Codeline|gm}} which is equal to 0.49148. We will use it to produce the prediction vectors. Only the first 4800 datapoints from {{Codeline|amplitude}} are used in order to compare the predicted values with the actual ones for the last 200 points. | |||
{{Code|Creating forecast points|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
steps = 200; | |||
forecast = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148, 'l', steps); | |||
forecast_noisy = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148, ... | |||
'dnoise', 10, 'l', steps); | |||
plot (amplitude(end-199:end), 'g;Actual Data;', ... | |||
forecast, 'r.;Forecast Data;',... | |||
forecast_noisy, 'bo;Forecast Data with 10% Dynamic Noise;'); | |||
</syntaxhighlight>}} | |||
[[File:tisean_nl_prediction_2.png|400px|center]] | |||
The difference between finding the proper {{Codeline|r}} and not finding it can be very small. <br/> | |||
The produced data is the best local zeroth order fit on the {{Codeline|amplitude.dat}} for {{Codeline|(m = 4, d = 6)}}. | |||
=== Nonlinear Noise Reduction === | |||
This tutorial show different methods of the 'Nonlinear Noise Reduction' section of the TISEAN documentation (located [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node22.html#SECTION00060000000000000000 here]). It shows the use of simple nonlinear noise reduction (function {{Codeline|lazy}}) and locally projective nonlinear noise reduction (function {{Codeline|ghkss}}). To start let's create noisy data to work with. | |||
{{Code|Creating a noisy henon map|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
hen = henon (10000); | |||
hen = hen(:,1); # We only need the first column | |||
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3)); | |||
</syntaxhighlight>}} | |||
This created a Henon map contaminated by 2% Gaussian noise à la TISEAN. In the tutorials and exercises on the TISEAN website this would be equivalent to calling {{Codeline|makenoise -%2}} on the Henon map.<br/> | |||
Next we will reduce the noise using simple nonlinear noise reduction {{Codeline|lazy}}. | |||
{{Code|Simple nonlinear noise reduction|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
clean = lazy (hen_noisy,7,-0.06,3); | |||
# Create delay vectors for both the clean and noisy data | |||
delay_clean = delay (clean); | |||
delay_noisy = delay (hen_noisy); | |||
# Plot both on one chart | |||
plot (delay_noisy(:,1), delay_noisy(:,2), 'b.;Noisy Data;','markersize',3,... | |||
delay_clean(:,1), delay_clean(:,2), 'r.;Clean Data;','markersize',3) | |||
</syntaxhighlight>}} | |||
[[File:tisean_nl_noisereduction.png|400px|center]] | |||
[[File: | On the chart created the red dots represent cleaned up data. It is much closer to the original than the noisy blue set.<br/> | ||
Now we will do the same with {{Codeline|ghkss}}. | |||
{{Code|Locally projective nonlinear noise reduction|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
clean = ghkss (hen,'m',7,'q',2,'r',0.05,'k',20,'i',2); | |||
</syntaxhighlight>}} | |||
The rest of the code is the same as the code used in the {{Codeline|lazy}} example. <br/> | |||
Once both results are compared it is quite obvious that for this particular example {{Codeline|ghkss}} is superior to {{Codeline|lazy}}. The TISEAN documentation points out that this is not always the case. | |||
[[File:tisean_nl_noisereduction_2.png|400px|center]] | |||
[[Category:Octave | === Lyapunov Exponents === | ||
Here I will demonstrate how to use the function {{Codeline|lyap_k}}. It estimates the maximal Lyapunov exponent from a time series (more information available from the TISEAN documentation located [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node27.html here]). In this tutorial we will estimate the maximal Lyapunov exponent for various embedding dimensions and then plot them. | |||
{{Code|Creating Lyapunov exponents|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create time series | |||
in = sin((1:2500).'./360) + cos((1:2500).'./180); | |||
# Estimate Lyapunov exponents | |||
mmax_val = 20 | |||
lyap_exp = lyap_k (in, 'mmin',2,'mmax',mmax_val,'d',6,'s',400,'t',500); | |||
</syntaxhighlight>}} | |||
In this function the output ({{Codeline|lyap_exp}} is a {{Codeline|5 x 20}} struct array. We will only use one row for the plot. | |||
{{Code|Plotting Lyapunov exponents|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
cla reset | |||
hold on | |||
for j=2:mmax_val | |||
plot (lyap_exp(1,j-1).exp(:,1),lyap_exp(1,j-1).exp(:,2),'r'); | |||
endfor | |||
xlabel ("t [flow samples]"); | |||
ylabel ("S(eps, embed, t)"); | |||
hold off | |||
</syntaxhighlight>}} | |||
[[File:lyap_k.png|400px|center]] | |||
=== Dimensions and Entropies === | |||
This section is discussed on the [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node29.html#SECTION00080000000000000000 TISEAN documentation page]. One of the functions discussed is {{Codeline|d2}}. It is used to estimate the correlation sum, correlation dimension and correlation entropy of a time series. The time series used here will be the Henon map. | |||
{{Code|Calculation correlation sum, dimension and entropy|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create maps | |||
hen = henon (10000); | |||
# Calculate the correlation sum, dimension and entropy | |||
vals = d2 (hen, 'd', 1, 'm', 5, 't',50); | |||
# Plot correlation sum | |||
subplot (2,3,1) | |||
do_plot_corr = @(x) loglog (x{1}(:,1),x{1}(:,2),'b'); | |||
hold on | |||
arrayfun (do_plot_corr, {vals.c2}); | |||
hold off | |||
xlabel ("Epsilon") | |||
ylabel ("Correlation sums") | |||
title ("c2"); | |||
# Plot correlation entropy | |||
subplot (2,3,4) | |||
do_plot_entrop = @(x) semilogx (x{1}(:,1),x{1}(:,2),'g'); | |||
hold on | |||
arrayfun (do_plot_entrop, {vals.h2}); | |||
hold off | |||
xlabel ("Epsilon") | |||
ylabel ("Correlation entropies"); | |||
title ("h2") | |||
# Plot correlation dimension | |||
subplot (2,3,[2 3 5 6]) | |||
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'r'); | |||
hold on | |||
arrayfun (do_plot_slope, {vals.d2}); | |||
hold off | |||
xlabel ("Epsilon") | |||
ylabel ("Local slopes") | |||
title ("d2"); | |||
</syntaxhighlight>}} | |||
[[File:d2_out.png|400px|center]] | |||
The output of {{Codeline|d2}} can be further processed using the following functions: {{Codeline|av_d2}}, {{Codeline|c2t}}, {{Codeline|c2g}}. This tutorial will show how to use {{Codeline|av_d2}} which smooths the output of {{Codeline|d2}} (usually used to smooth the "{{Codeline|d2}}" field of the output). | |||
{{Code|Smooth output of d2|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Smooth d2 output | |||
figure 2 | |||
smooth = av_d2 (vals,'a',2); | |||
# Plot the smoothed output | |||
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'b'); | |||
hold on | |||
arrayfun (do_plot_slope, {smooth.d2}); | |||
hold off | |||
xlabel ("Epsilon") | |||
ylabel ("Local slopes") | |||
title ("Smooth"); | |||
</syntaxhighlight>}} | |||
[[File:tisean_av_d2_out.png|400px|center]] | |||
Optionally the line "{{Codeline|figure 2}}" can be omitted, which will cause the smoothed version to be superimposed on the "raw" version that came straight from {{Codeline|d2}}. | |||
=== Testing for Nonlinearity === | |||
This section is discussed on the [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/docs/chaospaper/node35.html#SECTION00090000000000000000 TISEAN documentation page]. The focus of this section will be the function {{Codeline|surrogates}}. It uses surrogate data to determine weather data is nonlinear. Let us first create the input data which will be a stationary Gaussian linear stochastic process. It is measured by {{Codeline|s(xn) = xn^3}}. We then run it through {{Codeline|surrogates}} and plot the data. | |||
{{Code|Creating data from Gaussian process|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
# Create Gaussian process data | |||
g = zeros (2000,1); | |||
for i = 2:2000 | |||
g(i) = 0.7 * g(i-1) + (-6 + sum (rand ([size(1), 12]), 3)); | |||
endfor | |||
# Create a measurement of it | |||
spike = g.^3; | |||
# Create the surrogate | |||
sur = surrogates (spike); | |||
# Plot the data | |||
subplot (2,1,1) | |||
plot (spike,'g'); | |||
title ("spike") | |||
subplot (2,1,2) | |||
plot (sur,'b'); | |||
title ("surrogate") | |||
</syntaxhighlight>}} | |||
[[File:surrogate_tutorial.png|400px|center]] | |||
It is crucial that the length of the input to surrogates is factorizable by only 2,3 and 5. Therefore, if it is not the excess of data is truncated accordingly. Padding with zeros is not allowed. To solve this problem one can use {{Codeline|endtoend}}, and choose the best subset of the input data to be used to generate a surrogate. | |||
[[Category:Octave Forge]] | |||
== External links == | |||
* [https://bitbucket.org/josiah425/tisean Bitbucket repository ] where the porting is taking place. | |||
* [http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/ TISEAN package website] where the package is described along with references to literature, tutorials and manuals. | |||
Revision as of 19:23, 2 September 2018
Porting TISEAN
This section which focuses on demonstrating how the package is to be ported and what is the current state of that process is located in TISEAN_package:Procedure.
Tutorials
These tutorials are based on examples, tutorials and the articles located on the TISEAN website:
http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/.
This tutorial will utilize the following dataset:
Please download it as the tutorial will reference it.
False Nearest Neighbors
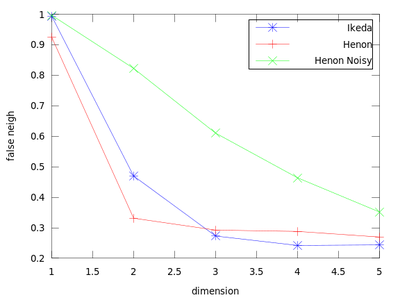
This function uses a method to determine the minimum sufficient embedding dimension. It is based on the False Nearest Neighbors section of the TISEAN documentation. As a demonstration we will create a plot that contains an Ikeda Map, a Henon Map and a Henon Map corrupted by 10% of Gaussian noise.
| Code: Analyzing false nearest neighbors |
# Create maps
ikd = ikeda (10000);
hen = henon (10000);
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));
# Create and plot false nearest neighbors
[dim_ikd, frac_ikd] = false_nearest (ikd(:,1));
[dim_hen, frac_hen] = false_nearest (hen(:,1));
[dim_hen_noisy, frac_hen_noisy] = false_nearest (hen_noisy(:,1));
plot (dim_ikd, frac_ikd, '-b*;Ikeda;',...
dim_hen, frac_hen, '-r+;Henon;',...
dim_hen_noisy, frac_hen_noisy, '-gx;Henon Noisy;');
|
The dim_* variables hold the dimension (so here 1:5), and frac_* contain the fraction of false nearest neighbors. From this chart we can obtain the sufficient embedding dimension for each system. For a Henon Map m = 2 is sufficient, but for an Ikeda map it is better to use m = 3.
Finding Unstable Periodic Orbits
Here I will demonstrate how to find unstable periodic orbits. This section is based on the TISEAN documentation chapter Finding unstable periodic orbits. We will start by finding these orbits using function upo.
| Code: Finding unstable periodic orbits |
# Create maps
hen = henon (1000);
hen = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));
# Find orbits
[lengths, data] = upo(hen(:,1), 2, 'p',6,'v',0.1, 'n', 100);
|
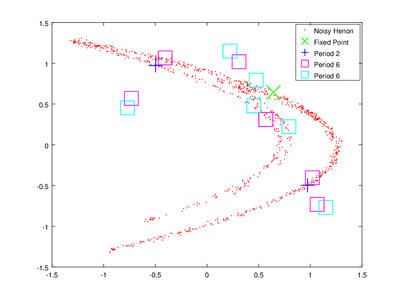
The vector lengths contains the size of each of the found orbits and data contains their coordinates. To obtain delay coordinates and plot these orbits onto the original data we will use upoembed.
| Code: Plotting unstable periodic orbits |
# Create delay coordinates for the orbits and data
up = upoembed (lengths, data, 1);
delay_hen = delay (hen(:,1));
# Plot all of the data
plot (delay_hen(:,1), delay_hen(:,2), 'r.;Noisy Henon;','markersize',2,...
up{4}(:,1), up{4}(:,2),'gx;Fixed Point;','markersize',20,'linewidth',1, ...
up{3}(:,1), up{3}(:,2),'b+;Period 2;','markersize',20,'linewidth',1, ...
up{2}(:,1), up{2}(:,2),'ms;Period 6;','markersize',20,'linewidth',1, ...
up{1}(:,1), up{1}(:,2),'cs;Period 6;','markersize',20,'linewidth',1);
|
The plotting options are passed to make the orbits more visible.
Nonlinear Prediction
In this section we will demonstrate some functions from the 'Nonlinear Prediction' chapter of the TISEAN documentation (located here). For now this section will only demonstrate functions that are connected to the Simple Nonlinear Prediction section.
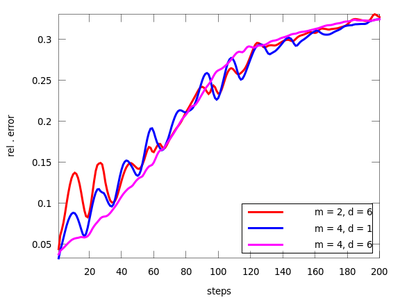
There are three functions in this section: lzo_test, lzo_gm and lzo_run. The first is used to estimate the forecast error for a set of chosen parameters, the second gives some global information about the fit and the third produces predicted points. Let us start with the first one (before starting this example remember to download 'amplitude.dat' from above and start Octave in the directory that contains it). The pairs of parameters (m,d) where chosen after the TISEAN documentation.
| Code: Analyzing forecast errors for various parameters |
# Load data
load amplitude.dat
# Create different forecast error results
steps = 200;
res1 = lzo_test (amplitude(1:end-200), 'm', 2, 'd', 6, 's', steps);
res2 = lzo_test (amplitude(1:end-200), 'm', 3, 'd', 6, 's', steps);
res3 = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 1, 's', steps);
res4 = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps);
plot (res1(:,1), res1(:,2), 'r;m = 2, d = 6;', ...
res2(:,1), res2(:,2), 'g;m = 3, d = 6;',...
res3(:,1), res3(:,2), 'b;m = 4, d = 1;',...
res4(:,1), res4(:,2), 'm;m = 4, d = 6;');
|
It seems that the last pair (m = 4, d = 6) is suitable. We will use it to determine the the best neighborhood to use when generating future points.
| Code: Determining the best neighborhood size using lzo_gm |
gm = lzo_gm (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps, 'rhigh', 20);
|
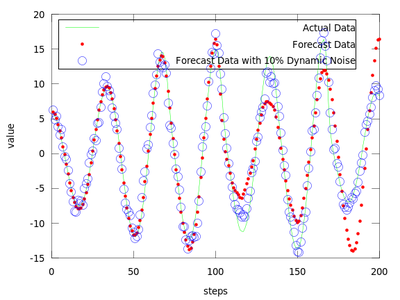
After analyzing gm it is easy to observe that the least error is for the first neighborhood size of gm which is equal to 0.49148. We will use it to produce the prediction vectors. Only the first 4800 datapoints from amplitude are used in order to compare the predicted values with the actual ones for the last 200 points.
| Code: Creating forecast points |
steps = 200;
forecast = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148, 'l', steps);
forecast_noisy = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148, ...
'dnoise', 10, 'l', steps);
plot (amplitude(end-199:end), 'g;Actual Data;', ...
forecast, 'r.;Forecast Data;',...
forecast_noisy, 'bo;Forecast Data with 10% Dynamic Noise;');
|
The difference between finding the proper r and not finding it can be very small.
The produced data is the best local zeroth order fit on the amplitude.dat for (m = 4, d = 6).
Nonlinear Noise Reduction
This tutorial show different methods of the 'Nonlinear Noise Reduction' section of the TISEAN documentation (located here). It shows the use of simple nonlinear noise reduction (function lazy) and locally projective nonlinear noise reduction (function ghkss). To start let's create noisy data to work with.
| Code: Creating a noisy henon map |
hen = henon (10000);
hen = hen(:,1); # We only need the first column
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));
|
This created a Henon map contaminated by 2% Gaussian noise à la TISEAN. In the tutorials and exercises on the TISEAN website this would be equivalent to calling makenoise -%2 on the Henon map.
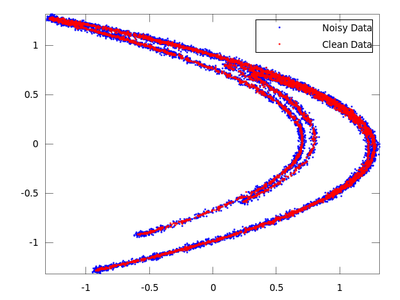
Next we will reduce the noise using simple nonlinear noise reduction lazy.
| Code: Simple nonlinear noise reduction |
clean = lazy (hen_noisy,7,-0.06,3);
# Create delay vectors for both the clean and noisy data
delay_clean = delay (clean);
delay_noisy = delay (hen_noisy);
# Plot both on one chart
plot (delay_noisy(:,1), delay_noisy(:,2), 'b.;Noisy Data;','markersize',3,...
delay_clean(:,1), delay_clean(:,2), 'r.;Clean Data;','markersize',3)
|
On the chart created the red dots represent cleaned up data. It is much closer to the original than the noisy blue set.
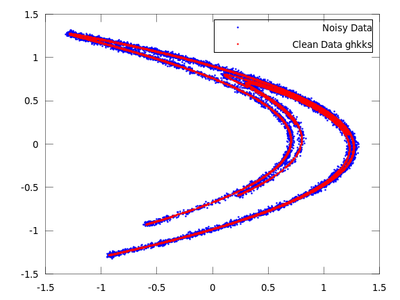
Now we will do the same with ghkss.
| Code: Locally projective nonlinear noise reduction |
clean = ghkss (hen,'m',7,'q',2,'r',0.05,'k',20,'i',2);
|
The rest of the code is the same as the code used in the lazy example.
Once both results are compared it is quite obvious that for this particular example ghkss is superior to lazy. The TISEAN documentation points out that this is not always the case.
Lyapunov Exponents
Here I will demonstrate how to use the function lyap_k. It estimates the maximal Lyapunov exponent from a time series (more information available from the TISEAN documentation located here). In this tutorial we will estimate the maximal Lyapunov exponent for various embedding dimensions and then plot them.
| Code: Creating Lyapunov exponents |
# Create time series
in = sin((1:2500).'./360) + cos((1:2500).'./180);
# Estimate Lyapunov exponents
mmax_val = 20
lyap_exp = lyap_k (in, 'mmin',2,'mmax',mmax_val,'d',6,'s',400,'t',500);
|
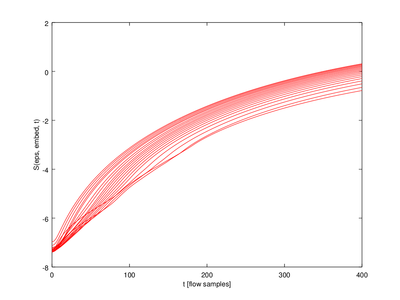
In this function the output (lyap_exp is a 5 x 20 struct array. We will only use one row for the plot.
| Code: Plotting Lyapunov exponents |
cla reset
hold on
for j=2:mmax_val
plot (lyap_exp(1,j-1).exp(:,1),lyap_exp(1,j-1).exp(:,2),'r');
endfor
xlabel ("t [flow samples]");
ylabel ("S(eps, embed, t)");
hold off
|
Dimensions and Entropies
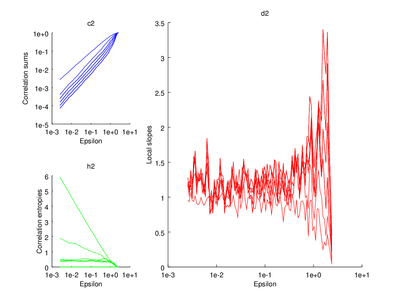
This section is discussed on the TISEAN documentation page. One of the functions discussed is d2. It is used to estimate the correlation sum, correlation dimension and correlation entropy of a time series. The time series used here will be the Henon map.
| Code: Calculation correlation sum, dimension and entropy |
# Create maps
hen = henon (10000);
# Calculate the correlation sum, dimension and entropy
vals = d2 (hen, 'd', 1, 'm', 5, 't',50);
# Plot correlation sum
subplot (2,3,1)
do_plot_corr = @(x) loglog (x{1}(:,1),x{1}(:,2),'b');
hold on
arrayfun (do_plot_corr, {vals.c2});
hold off
xlabel ("Epsilon")
ylabel ("Correlation sums")
title ("c2");
# Plot correlation entropy
subplot (2,3,4)
do_plot_entrop = @(x) semilogx (x{1}(:,1),x{1}(:,2),'g');
hold on
arrayfun (do_plot_entrop, {vals.h2});
hold off
xlabel ("Epsilon")
ylabel ("Correlation entropies");
title ("h2")
# Plot correlation dimension
subplot (2,3,[2 3 5 6])
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'r');
hold on
arrayfun (do_plot_slope, {vals.d2});
hold off
xlabel ("Epsilon")
ylabel ("Local slopes")
title ("d2");
|
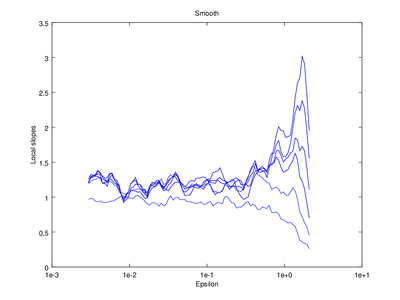
The output of d2 can be further processed using the following functions: av_d2, c2t, c2g. This tutorial will show how to use av_d2 which smooths the output of d2 (usually used to smooth the "d2" field of the output).
| Code: Smooth output of d2 |
# Smooth d2 output
figure 2
smooth = av_d2 (vals,'a',2);
# Plot the smoothed output
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'b');
hold on
arrayfun (do_plot_slope, {smooth.d2});
hold off
xlabel ("Epsilon")
ylabel ("Local slopes")
title ("Smooth");
|
Optionally the line "figure 2" can be omitted, which will cause the smoothed version to be superimposed on the "raw" version that came straight from d2.
Testing for Nonlinearity
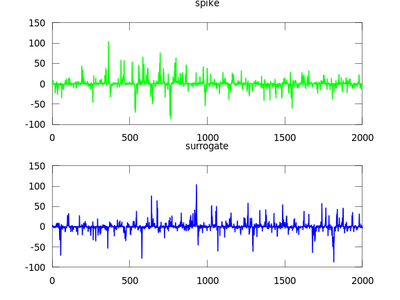
This section is discussed on the TISEAN documentation page. The focus of this section will be the function surrogates. It uses surrogate data to determine weather data is nonlinear. Let us first create the input data which will be a stationary Gaussian linear stochastic process. It is measured by s(xn) = xn^3. We then run it through surrogates and plot the data.
| Code: Creating data from Gaussian process |
# Create Gaussian process data
g = zeros (2000,1);
for i = 2:2000
g(i) = 0.7 * g(i-1) + (-6 + sum (rand ([size(1), 12]), 3));
endfor
# Create a measurement of it
spike = g.^3;
# Create the surrogate
sur = surrogates (spike);
# Plot the data
subplot (2,1,1)
plot (spike,'g');
title ("spike")
subplot (2,1,2)
plot (sur,'b');
title ("surrogate")
|
It is crucial that the length of the input to surrogates is factorizable by only 2,3 and 5. Therefore, if it is not the excess of data is truncated accordingly. Padding with zeros is not allowed. To solve this problem one can use endtoend, and choose the best subset of the input data to be used to generate a surrogate.
External links
- Bitbucket repository where the porting is taking place.
- TISEAN package website where the package is described along with references to literature, tutorials and manuals.