Interval package
The interval package provides data types and fundamental operations for real valued interval arithmetic based on the common floating-point format “binary64” a. k. a. double-precision. It aims to be standard compliant with the (upcoming) IEEE 1788 and therefore implements the set-based interval arithmetic flavor. Interval arithmetic produces mathematically proven numerical results.
Warning: The package has not yet been released. If you want to experience the development version, you may (1) install the (currently deprecated) fenv package, (2) download a snapshot version of the interval package, (3) navigate to the inst/ subfolder and run octave.
Motivation
Give a digital computer a problem in arithmetic, and it will grind away methodically, tirelessly, at gigahertz speed, until ultimately it produces the wrong answer. … An interval computation yields a pair of numbers, an upper and a lower bound, which are guaranteed to enclose the exact answer. Maybe you still don’t know the truth, but at least you know how much you don’t know.—Brian Hayes, DOI: 10.1511/2003.6.484
| Standard floating point arithmetic | Interval arithmetic |
|---|---|
octave:1> 19 * 0.1 - 2 + 0.1 ans = 1.3878e-16 |
octave:1> x = infsup ("0.1");
octave:2> 19 * x - 2 + x
ans ⊂ [-3.1918911957973251e-16, +1.3877787807814457e-16]
|
Floating point arithmetic, as specified by IEEE 754, is available in almost every computer system today. It is wide-spread, implemented in common hardware and integral part in programming languages. For example, the extended precision format is the default numeric data type in GNU Octave. Benefits are obvious: The results of arithmetic operations are well-defined and comparable between different systems and computation is highly efficient.
However, there are some downsides of floating point arithmetic in practice, which will eventually produce errors in computations.
- Floating point arithmetic is often used mindlessly by developers. [1] [2]
- The binary data types categorically are not suitable for doing financial computations. Very often representational errors are introduced when using “real world” decimal numbers. [3]
- Even if the developer would be proficient, most developing environments / technologies limit floating point arithmetic capabilities to a very limited subset of IEEE 754: Only one or two data types, no rounding modes, … [4]
- Results are hardly predictable. [5] All operations produce the best possible accuracy at runtime, this is how floating-point works. Contrariwise, financial computer systems typically use a fixed-point arithmetic (COBOL, PL/I, …), where overflow and rounding can be precisely predicted at compile-time.
- If you do not know the technical details, cf. first bullet, you ignore the fact that the computer lies to you in many situations. For example, when looking at numerical output and the computer says “
ans = 0.1,” this is not absolutely correct. In fact, the value is only close enough to the value 0.1. Additionally, many functions produce limit values (∞ × −∞ = −∞, ∞ ÷ 0 = ∞, ∞ ÷ −0 = −∞, log (0) = −∞), which is sometimes (but not always!) useful when overflow and underflow occur.
Interval arithmetic addresses above problems in its very special way and introduces new possibilities for algorithms. For example, the interval newton method is able to find all zeros of a particular function.
Theory
Moore's fundamental theroem of interval arithmetic
Let y = f(x) be the result of interval-evaluation of f over a box x = (x1, … , xn) using any interval versions of its component library functions. Then
- In all cases, y contains the range of f over x, that is, the set of f(x) at points of x where it is defined: y ⊇ Rge(f | x) = {f(x) | x ∈ x ∩ Dom(f) }
- If also each library operation in f is everywhere defined on its inputs, while evaluating y, then f is everywhere defined on x, that is Dom(f) ⊇ x.
- If in addition, each library operation in f is everywhere continuous on its inputs, while evaluating y, then f is everywhere continuous on x.
- If some library operation in f is nowhere defined on its inputs, while evaluating y, then f is nowhere defined on x, that is Dom(f) ∩ x = Ø.
Quick start introduction
Input and output
Before exercising interval arithmetic, interval objects must be created, typically from non-interval data. There are interval constants empty and entire and the class constructors infsup for bare intervals and infsupdec for decorated intervals. The class constructors are very sophisticated and can be used with several kinds of parameters: Interval boundaries can be given by numeric values or string values with decimal numbers. Also it is possible to use so called interval literals with square brackets.
octave:1> infsup (1)
ans = [1]
octave:2> infsup (1, 2)
ans = [1, 2]
octave:3> infsup ("3", "4")
ans = [3, 4]
octave:4> infsup ("1.1")
ans ⊂ [1.0999999999999998, 1.1000000000000001]
octave:5> infsup ("[5, 6.5]")
ans = [5, 6.5]
octave:6> infsup ("[5.8e-17]")
ans ⊂ [5.799999999999999e-17, 5.800000000000001e-17]
It is possible to access the exact numeric interval boundaries with the functions inf and sup. The default text representation of intervals can be created with intervaltotext. The default text representation is not guaranteed to be exact (see function intervaltoexact), because this would massively spam console output. For example, the exact text representation of realmin would be over 700 decimal places long! However, the default text representation is correct as it guarantees to contain the actual boundaries and is accurate enough to separate different boundaries.
octave:7> infsup (1, 1 + eps) ans ⊂ [1, 1.0000000000000003] octave:8> infsup (1, 1 + 2 * eps) ans ⊂ [1, 1.0000000000000005]
Warning: Decimal fractions as well as numbers of high magnitude (> 253) should always be passed as a string to the constructor. Otherwise it is possible, that GNU Octave introduces conversion errors when the numeric literal is converted into floating-point format before it is passed to the constructor.
octave:9> infsup (0.2) ans ⊂ [.20000000000000001, .20000000000000002] octave:10> infsup ("0.2") ans ⊂ [.19999999999999998, .20000000000000002]
For convenience it is possible to implicitly call the interval constructor during all interval operations if at least one input already is an interval object.
octave:11> infsup ("17.7") + 1
ans ⊂ [18.699999999999999, 18.700000000000003]
octave:12> ans + "[0, 2]"
ans ⊂ [18.699999999999999, 20.700000000000003]
Decorations
With the subclass infsupdec it is possible to extend interval arithmetic with a decoration system. Every interval and intermediate result will additionally carry a decoration, which may provide additional information about the final result. The following decorations are available:
| Decoration | Bounded | Continuous | Defined | Definition |
|---|---|---|---|---|
| com (common) |
✓ | ✓ | ✓ | x is a bounded, nonempty subset of Dom(f); f is continuous at each point of x; and the computed interval f(x) is bounded |
| dac (defined & continuous) |
✓ | ✓ | x is a nonempty subset of Dom(f); and the restriction of f to x is continuous | |
| def (defined) |
✓ | x is a nonempty subset of Dom(f) | ||
| trv (trivial) |
always true (so gives no information) | |||
| ill (ill-formed) |
Not an interval, at least one interval constructor failed during the course of computation |
In the following example, all decoration information is lost when the interval is possibly divided by zero, i. e., the overall function is not guaranteed to be defined for all possible inputs.
octave:1> infsupdec (3, 4) ans = [3, 4]_com octave:2> ans + 12 ans = [15, 16]_com octave:3> ans / "[0, 2]" ans = [7.5, Inf]_trv
Arithmetic operations
The interval packages comprises many interval arithmetic operations. Function names match GNU Octave standard functions where applicable, and follow recommendations by IEEE 1788 otherwise. It is possible to look up all functions by their corresponding IEEE 1788 name in the index Template:Citation needed.
Arithmetic functions in a set-based interval arithmetic follow these rules: Intervals are sets. They are subsets of the set of real numbers. The interval version of an elementary function such as sin(x) is essentially the natural extension to sets of the corresponding point-wise function on real numbers. That is, the function is evaluated for each number in the interval where the function is defined and the result must be an enclosure of all possible values that may occur.
One operation that should be noted is the fma function (fused multiply and add). It computes x × y + z in a single step and is much slower than multiplication followed by addition. However, it is more accurate and therefore preferred in some situations.
octave:1> sin (infsup (0.5)) ans ⊂ [.47942553860420294, .47942553860420307] octave:2> pow (infsup (2), infsup (3, 4)) ans = [8, 16] octave:3> atan2 (infsup (1), infsup (1)) ans ⊂ [.7853981633974479, .7853981633974487]
Reverse arithmetic operations
Some arithmetic functions also provide reverse mode operations. That is inverse functions with interval constraints. For example the sqrrev can compute the inverse of the sqr function on intervals.
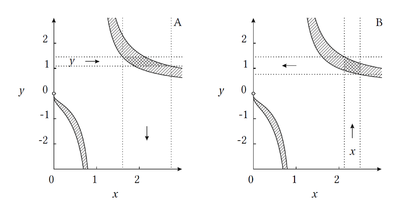
In the following example, we compute the constraints for base and exponent of the power function pow as shown in the figure.
octave:1> x = powrev1 (infsup ("[1.1, 1.45]"), infsup (2, 3))
x ⊂ [1.6128979635153644, 2.7148547265657923]
octave:2> y = powrev2 (infsup ("[2.14, 2.5]"), infsup (2, 3))
y ⊂ [.7564707973660299, 1.4440113978403289]
Numerical operations
Boolean operations
Error handling
Due to the nature of set-based interval arithmetic, you should never observe errors during computation. If you do, there either is a bug in the code or there are unsupported data types.
octave:1> infsup (2, 3) / 0 ans = [Empty] octave:2> infsup (0) ^ infsup (0) ans = [Empty]
However, the interval constructors can produce errors depending on the input. The infsup constructor will fail if the interval boundaries are invalid. Contrariwise, the infsupdec constructor will only issue a warning and return a [NaI], which will propagate and survive through computations.
octave:3> infsup (3, 2) + 1 error: illegal interval boundaries: infimum greater than supremum … (call stack) … octave:3> infsupdec (3, 2) + 1 warning: illegal interval boundaries: infimum greater than supremum ans = [NaI]
Related work
For MATLAB there is a popular interval arithmetic toolbox INTLAB by Siegfried Rump (member of IEEE P1788). It had been free (as in free beer) for academic use in the past, but no longer is. Its origin dates back to 1999, so it is well tested and comprises a lot of functionality, especially for vector / matrix operations. INTLAB is not compatible with GNU Octave. I don't know if INTLAB is or will be compliant with IEEE 1788.
For C++ there is an interval library libIEEE1788 by Marco Nehmeier (member of IEEE P1788). It aims to be standard compliant with IEEE 1788, but is not complete yet.
For Java there is a library jinterval by Dmitry Nadezhin (member of IEEE P1788). It aims to be standard compliant with IEEE 1788, but is not complete yet.