Interval package: Difference between revisions
m (→Motivation: Added bullet: System dependent results) |
m (→What to expect: Added runtime information) |
||
| Line 51: | Line 51: | ||
''Why is the interval package slow?'' | ''Why is the interval package slow?'' | ||
All arithmetic interval operations are simulated in high-level octave language using C99 | All arithmetic interval operations are simulated in high-level octave language using C99 or multi-precision floating-point routines, which is a lot slower than a hardware implementation [https://books.google.de/books?id=JTc4XdXFnQIC&pg=PA61]. Building interval arithmetic operations from floating-point routines is easy for simple monotonic functions, e. g., addition and subtraction, but is complex for others, e. g., [http://exp.ln0.de/heimlich-power-2011.htm interval power function], atan2, or [[#Reverse_arithmetic_operations|reverse functions]]. For some interval operations it is not even possible to rely on floating-point routines, since not all required routines are available in C99 or BLAS. | ||
Great algorithms and optimizations exist for matrix arithmetic in GNU | Great algorithms and optimizations exist for floating-point matrix arithmetic in GNU Octave. Good interval versions of these still have to be found and implemented. For example, multiplication of matrices with many elements becomes unfeasible as it takes a lot of time. (For that purpose one could use the [[#Related work|INTLAB toolbox]], which uses a less accurate arithmetic) | ||
{| class="wikitable" style="margin: auto; align:right" | |||
|+align="bottom" | Approximate runtime (wall clock time in seconds) on an Intel® Core™ i5-4340M CPU | |||
!Matrix dimension | |||
!Interval <code>plus</code> | |||
!Interval <code>log</code> | |||
!Interval <code>mtimes</code> | |||
!Interval <code>inv</code> | |||
|- | |||
|align="right"| 10 | |||
|align="right"| < 0.1 | |||
|align="right"| < 0.1 | |||
|align="right"| 0.4 | |||
|align="right"| 3.3 | |||
|- | |||
|align="right"| 20 | |||
|align="right"| < 0.1 | |||
|align="right"| < 0.1 | |||
|align="right"| 2.3 | |||
|style="text-align:right; font-weight: bold; color:orange"| 32.3 | |||
|- | |||
|align="right"| 30 | |||
|align="right"| < 0.1 | |||
|align="right"| < 0.1 | |||
|align="right"| 7.0 | |||
|style="text-align:right; font-weight: bold; color:red"| 142.1 | |||
|- | |||
|align="right"| 40 | |||
|align="right"| < 0.1 | |||
|align="right"| 0.1 | |||
|align="right"| 15.6 | |||
|- | |||
|align="right"| 50 | |||
|align="right"| 0.1 | |||
|align="right"| 0.2 | |||
|style="text-align:right; font-weight: bold; color:orange"| 29.1 | |||
|} | |||
''Why is the interval package accurate?'' | ''Why is the interval package accurate?'' | ||
The GNU Octave builtin floating-point routines are not useful for interval arithmetic: Their results depend on hardware, system libraries and compilation options. | |||
The interval package handles all arithmetic functions with the help of the [http://www.mpfr.org/ GNU MPFR library]. With MPFR it is possible to compute system-independent, valid and tight enclosures of the correct results. | The interval package handles all arithmetic functions with the help of the [http://www.mpfr.org/ GNU MPFR library]. With MPFR it is possible to compute system-independent, valid and tight enclosures of the correct results. | ||
Revision as of 16:43, 18 January 2015
The interval package provides data types and fundamental operations for real valued interval arithmetic based on the common floating-point format “binary64” a. k. a. double-precision. It aims to be standard compliant with the (upcoming) IEEE 1788 and therefore implements the set-based interval arithmetic flavor. Interval arithmetic produces mathematically proven numerical results.
Warning: The package has not yet been released. If you want to experience the development version, you may (1) download a snapshot version of the interval package, (2) install the development library of MPFR for your system, (3) execute make install in the src/ subfolder, (5) navigate to the inst/ subfolder and run octave.
Motivation
Give a digital computer a problem in arithmetic, and it will grind away methodically, tirelessly, at gigahertz speed, until ultimately it produces the wrong answer. … An interval computation yields a pair of numbers, an upper and a lower bound, which are guaranteed to enclose the exact answer. Maybe you still don’t know the truth, but at least you know how much you don’t know.—Brian Hayes, DOI: 10.1511/2003.6.484
| Standard floating point arithmetic | Interval arithmetic |
|---|---|
octave:1> 19 * 0.1 - 2 + 0.1 ans = 1.3878e-16 |
octave:1> x = infsup ("0.1");
octave:2> 19 * x - 2 + x
ans ⊂ [-3.1918911957973251e-16, +1.3877787807814457e-16]
|
Floating-point arithmetic, as specified by IEEE 754, is available in almost every computer system today. It is wide-spread, implemented in common hardware and integral part in programming languages. For example, the double-precision format is the default numeric data type in GNU Octave. Benefits are obvious: The results of arithmetic operations are well-defined and comparable between different systems and computation is highly efficient.
However, there are some downsides of floating-point arithmetic in practice, which will eventually produce errors in computations.
- Floating-point arithmetic is often used mindlessly by developers. [1] [2]
- The binary data types categorically are not suitable for doing financial computations. Very often representational errors are introduced when using “real world” decimal numbers. [3]
- Even if the developer would be proficient, most developing environments / technologies limit floating-point arithmetic capabilities to a very limited subset of IEEE 754: Only one or two data types, no rounding modes, missing functions … [4]
- Results are hardly predictable. [5] All operations produce the best possible accuracy at runtime, this is how a floating point works. Contrariwise, financial computer systems typically use a fixed-point arithmetic (COBOL, PL/I, …), where overflow and rounding can be precisely predicted at compile-time.
- Results are system dependent. All but the most basic floating-point operations are not guaranteed to be accurate and produce different results depending on low level libraries and hardware. [6] [7]
- If you do not know the technical details (cf. first bullet) you ignore the fact that the computer lies to you in many situations. For example, when looking at numerical output and the computer says “
ans = 0.1,” this is not absolutely correct. In fact, the value is only close enough to the value 0.1. Additionally, many functions produce limit values (∞ × −∞ = −∞, ∞ ÷ 0 = ∞, ∞ ÷ −0 = −∞, log (0) = −∞), which is sometimes (but not always!) useful when overflow and underflow occur.
Interval arithmetic addresses above problems in its very special way and introduces new possibilities for algorithms. For example, the interval newton method is able to find all zeros of a particular function.
Theory
Moore's fundamental theroem of interval arithmetic
Let y = f(x) be the result of interval-evaluation of f over a box x = (x1, … , xn) using any interval versions of its component library functions. Then
- In all cases, y contains the range of f over x, that is, the set of f(x) at points of x where it is defined: y ⊇ Rge(f | x) = {f(x) | x ∈ x ∩ Dom(f) }
- If also each library operation in f is everywhere defined on its inputs, while evaluating y, then f is everywhere defined on x, that is Dom(f) ⊇ x.
- If in addition, each library operation in f is everywhere continuous on its inputs, while evaluating y, then f is everywhere continuous on x.
- If some library operation in f is nowhere defined on its inputs, while evaluating y, then f is nowhere defined on x, that is Dom(f) ∩ x = Ø.
Online Introductions
What to expect
The interval arithmetic provided by this interval package is slow, but accurate.
Why is the interval package slow? All arithmetic interval operations are simulated in high-level octave language using C99 or multi-precision floating-point routines, which is a lot slower than a hardware implementation [8]. Building interval arithmetic operations from floating-point routines is easy for simple monotonic functions, e. g., addition and subtraction, but is complex for others, e. g., interval power function, atan2, or reverse functions. For some interval operations it is not even possible to rely on floating-point routines, since not all required routines are available in C99 or BLAS.
Great algorithms and optimizations exist for floating-point matrix arithmetic in GNU Octave. Good interval versions of these still have to be found and implemented. For example, multiplication of matrices with many elements becomes unfeasible as it takes a lot of time. (For that purpose one could use the INTLAB toolbox, which uses a less accurate arithmetic)
| Matrix dimension | Interval plus
|
Interval log
|
Interval mtimes
|
Interval inv
|
|---|---|---|---|---|
| 10 | < 0.1 | < 0.1 | 0.4 | 3.3 |
| 20 | < 0.1 | < 0.1 | 2.3 | 32.3 |
| 30 | < 0.1 | < 0.1 | 7.0 | 142.1 |
| 40 | < 0.1 | 0.1 | 15.6 | |
| 50 | 0.1 | 0.2 | 29.1 |
Why is the interval package accurate? The GNU Octave builtin floating-point routines are not useful for interval arithmetic: Their results depend on hardware, system libraries and compilation options.
The interval package handles all arithmetic functions with the help of the GNU MPFR library. With MPFR it is possible to compute system-independent, valid and tight enclosures of the correct results.
Quick start introduction
Input and output
Before exercising interval arithmetic, interval objects must be created from non-interval data. There are interval constants empty and entire and the class constructors infsup for bare intervals and infsupdec for decorated intervals. The class constructors are very sophisticated and can be used with several kinds of parameters: Interval boundaries can be given by numeric values or string values with decimal numbers. Also it is possible to use so called interval literals with square brackets.
octave:1> infsup (1)
ans = [1]
octave:2> infsup (1, 2)
ans = [1, 2]
octave:3> infsup ("3", "4")
ans = [3, 4]
octave:4> infsup ("1.1")
ans ⊂ [1.0999999999999998, 1.1000000000000001]
octave:5> infsup ("[5, 6.5]")
ans = [5, 6.5]
octave:6> infsup ("[5.8e-17]")
ans ⊂ [5.799999999999999e-17, 5.800000000000001e-17]
It is possible to access the exact numeric interval boundaries with the functions inf and sup. The shown text representation of intervals can be created with intervaltotext. The default text representation is not guaranteed to be exact (see function intervaltoexact for that purpose), because this would massively spam console output. For example, the exact text representation of realmin would be over 700 decimal places long! However, the default text representation is correct as it guarantees to contain the actual boundaries and is accurate enough to separate different boundaries.
octave:7> infsup (1, 1 + eps) ans ⊂ [1, 1.0000000000000003] octave:8> infsup (1, 1 + 2 * eps) ans ⊂ [1, 1.0000000000000005]
Warning: Decimal fractions as well as numbers of high magnitude (> 253) should always be passed as a string to the constructor. Otherwise it is possible, that GNU Octave introduces conversion errors when the numeric literal is converted into floating-point format before it is passed to the constructor.
octave:9> infsup (0.2) ans ⊂ [.20000000000000001, .20000000000000002] octave:10> infsup ("0.2") ans ⊂ [.19999999999999998, .20000000000000002]
For convenience it is possible to implicitly call the interval constructor during all interval operations if at least one input already is an interval object.
octave:11> infsup ("17.7") + 1
ans ⊂ [18.699999999999999, 18.700000000000003]
octave:12> ans + "[0, 2]"
ans ⊂ [18.699999999999999, 20.700000000000003]
Specialized interval constructors
Above mentioned interval construction with decimal numbers or numeric data is straightforward. Beyond that, there are more ways to define intervals or interval boundaries.
- Hexadecimal-floating-constant form: Each interval boundary may be defined by a hexadecimal number (optionally containing a point) and an exponent field with an integral power of two as defined by the C99 standard (ISO/IEC9899, N1256, §6.4.4.2). This can be used as a convenient way to define interval boundaries in double-precision, because the hexadecimal form is much shorter than the decimal representation of many numbers.
- Rational literals: Each interval boundary may be defined as a fraction of two decimal numbers. This is especially useful if interval boundaries shall be tightest enclosures of fractions, that would be hard to write down as a decimal number.
- Uncertain form: The interval as a whole can be defined by a midpoint or upper/lower boundary and an integral number of “units in last place” (ULPs) as an uncertainty. The format is
m?ruE, wheremis a mantissa in decimal,ris either empty (which means ½ ULP) or is a non-negative decimal integral ULP count or is the?character (for unbounded intervals),uis either empty (symmetrical uncertainty of r ULPs in both directions) or is eitheru(up) ord(down),Eis either empty or an exponent field comprising the characterefollowed by a decimal integer exponent (base 10).
octave:13> infsup ("0x1.999999999999Ap-4")
ans ⊂ [.1, .10000000000000001]
octave:14> infsup ("1/3", "7/9")
ans ⊂ [.33333333333333331, .7777777777777778]
octave:15> infsup ("121.2?")
ans ⊂ [121.14999999999999, 121.25]
octave:16> infsup ("5?32e2")
ans = [-2700, +3700]
octave:17> infsup ("-42??u")
ans = [-42, +Inf]
Interval vectors and matrices
Vectors and matrices of intervals can be created by passing numerical matrices, char vectors or cell arrays to the infsup constructor. With cell arrays it is also possible to mix several types of boundaries.
octave:18> M = infsup (magic (3))
M = 3×3 interval matrix
[8] [1] [6]
[3] [5] [7]
[4] [9] [2]
octave:19> infsup (magic (3), magic (3) + 1)
ans = 3×3 interval matrix
[8, 9] [1, 2] [6, 7]
[3, 4] [5, 6] [7, 8]
[4, 5] [9, 10] [2, 3]
octave:20> infsup (["0.1"; "0.2"; "0.3"; "0.4"; "0.5"])
ans ⊂ 5×1 interval vector
[.09999999999999999, .10000000000000001]
[.19999999999999998, .20000000000000002]
[.29999999999999998, .30000000000000005]
[.39999999999999996, .40000000000000003]
[.5]
octave:21> infsup ({1, eps; "4/7", "pi"}, {2, 1; "e", "0xff"})
ans ⊂ 2×2 interval matrix
[1, 2] [2.220446049250313e-16, 1]
[.5714285714285713, 2.7182818284590456] [3.1415926535897931, 255]
When matrices are resized using subscripted assignment, any implicit new matrix elements will carry an empty interval.
octave:22> M (4, 4) = 42
M = 4×4 interval matrix
[8] [1] [6] [Empty]
[3] [5] [7] [Empty]
[4] [9] [2] [Empty]
[Empty] [Empty] [Empty] [42]
Note: Whilst most functions (size, isvector, ismatrix, …) work as expected on interval data types, the function isempty is evaluated element-wise and checks if an interval equals the empty set.
octave:23> builtin ("isempty", empty ()), isempty (empty ())
ans = 0
ans = 1
Decorations
With the subclass infsupdec it is possible to extend interval arithmetic with a decoration system. Every interval and intermediate result will additionally carry a decoration, which may provide additional information about the final result. The following decorations are available:
| Decoration | Bounded | Continuous | Defined | Definition |
|---|---|---|---|---|
| com (common) |
✓ | ✓ | ✓ | x is a bounded, nonempty subset of Dom(f); f is continuous at each point of x; and the computed interval f(x) is bounded |
| dac (defined & continuous) |
✓ | ✓ | x is a nonempty subset of Dom(f); and the restriction of f to x is continuous | |
| def (defined) |
✓ | x is a nonempty subset of Dom(f) | ||
| trv (trivial) |
always true (so gives no information) | |||
| ill (ill-formed) |
Not an interval, at least one interval constructor failed during the course of computation |
In the following example, all decoration information is lost when the interval is possibly divided by zero, i. e., the overall function is not guaranteed to be defined for all possible inputs.
octave:1> infsupdec (3, 4) ans = [3, 4]_com octave:2> ans + 12 ans = [15, 16]_com octave:3> ans / "[0, 2]" ans = [7.5, Inf]_trv
Arithmetic operations
The interval packages comprises many interval arithmetic operations. Function names match GNU Octave standard functions where applicable, and follow recommendations by IEEE 1788 otherwise. It is possible to look up all functions by their corresponding IEEE 1788 name in the index.
Arithmetic functions in a set-based interval arithmetic follow these rules: Intervals are sets. They are subsets of the set of real numbers. The interval version of an elementary function such as sin(x) is essentially the natural extension to sets of the corresponding point-wise function on real numbers. That is, the function is evaluated for each number in the interval where the function is defined and the result must be an enclosure of all possible values that may occur.
One operation that should be noted is the fma function (fused multiply and add). It computes x × y + z in a single step and is much slower than multiplication followed by addition. However, it is more accurate and therefore preferred in some situations.
octave:1> sin (infsup (0.5)) ans ⊂ [.47942553860420294, .47942553860420301] octave:2> pow (infsup (2), infsup (3, 4)) ans = [8, 16] octave:3> atan2 (infsup (1), infsup (1)) ans ⊂ [.7853981633974482, .7853981633974484]
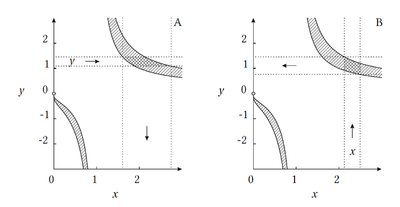
Reverse arithmetic operations
Some arithmetic functions also provide reverse mode operations. That is inverse functions with interval constraints. For example the sqrrev can compute the inverse of the sqr function on intervals. The syntax is sqrrev (C, X) and will compute the enclosure of all numbers x ∈ X that fulfill the constraint x² ∈ C.
In the following example, we compute the constraints for base and exponent of the power function pow as shown in the figure.
octave:1> x = powrev1 (infsup ("[1.1, 1.45]"), infsup (2, 3))
x ⊂ [1.6128979635153646, 2.7148547265657915]
octave:2> y = powrev2 (infsup ("[2.14, 2.5]"), infsup (2, 3))
y ⊂ [.7564707973660299, 1.4440113978403284]
Numerical operations
Some operations on intervals do not return an interval enclosure, but a single number (in double-precision). Most important are inf and sup, which return the lower and upper interval boundaries.
More such operations are mid (approximation of the interval's midpoint), wid (approximation of the interval's width), rad (approximation of the interval's radius), mag and mig.
Boolean operations
Interval comparison operations produce boolean results. While some comparisons are especially for intervals (subset, interior, ismember, isempty, disjoint, …) others are extensions of simple numerical comparison. For example, the less-or-equal comparison is mathematically defined as ∀a ∃b a ≤ b ∧ ∀b ∃a a ≤ b.
octave:1> infsup (1, 3) <= infsup (2, 4) ans = 1
Matrix operations
Above mentioned operations can also be applied element-wise to interval vectors and matrices. Many operations use vectorization techniques.
In addition, there are matrix operations on interval matrices. These operations comprise: tight dot product, tight matrix multiplication, tight vector sums, matrix inversion, matrix powers, and solving linear systems. As a result of missing hardware / low-level library support and missing optimizations, these operations are quite slow compared to familiar operations in floating-point arithmetic.
octave:1> A = infsup ([1, 2, 3; 4, 0, 0; 0, 0, 1]); A (2, 3) = "[0, 6]"
A = 3×3 interval matrix
[1] [2] [3]
[4] [0] [0, 6]
[0] [0] [1]
octave:2> B = inv (A)
B = 3×3 interval matrix
[0] [.25] [-1.5, 0]
[.5] [-.125] [-1.5, -.75]
[0] [0] [1]
octave:3> A * B
ans = 3×3 interval matrix
[1] [0] [-1.5, +1.5]
[0] [1] [-6, +6]
[0] [0] [1]
octave:4> A = infsup (magic (3)) A = 3×3 interval matrix [8] [1] [6] [3] [5] [7] [4] [9] [2] octave:5> c = A \ [3; 4; 5] c ⊂ 3×1 interval vector [.18333333333333323, .18333333333333344] [.43333333333333318, .43333333333333346] [.18333333333333323, .18333333333333344] octave:6> A * c ans ⊂ 3×1 interval vector [2.9999999999999982, 3.0000000000000018] [3.9999999999999982, 4.0000000000000018] [4.9999999999999973, 5.0000000000000018]
Notes on linear systems
A system of linear equations in the form Ax = b with intervals can be seen as a range of classical linear systems, which can be solved simultaneously. Whereas classical algorithms compute an approximation for a single solution of a single linear system, interval algorithms compute an enclosure for all possible solutions of (possibly several) linear systems. Some characteristics should definitely be known when linear interval systems are solved:
- If the linear system is underdetermined and has infinitely many solutions, the interval solution will be unbound in at least one of its coordinates. Contrariwise, from an unbound result it can not be concluded whether the linear system is underdetermined or has solutions.
- If the interval result is empty in at least one of its coordinates, the linear system is guaranteed to be underdetermined and has no solutions. Contrariwise, from a non-empty result it can not be concluded whether all or some of the systems have solutions or not.
- Wide intervals within the matrix A can easily lead to a superposition of cases, where the rank of A is no longer unique. If the linear interval system contains cases of linear independent equations as well as linear dependent equations, the resulting enclosure of solutions will inevitably be very broad.
- Due to the dependency problem in interval arithmetic, it may happen that the current solving algorithm produces poor results for some inputs.
However, solving linear systems with interval arithmetic can produce useful results in many cases and automatically carries a guaranty for error boundaries. Additionally, it can give better information than the floating-point variants for some cases.
| Standard floating point arithmetic | Interval arithmetic |
|---|---|
octave:1> A = [1, 0; 2, 0]; octave:2> A \ [3; 0] # no solution warning: matrix singular to machine precision, rcond = 0 ans = 0.60000 0.00000 octave:3> A \ [4; 8] # many solutions ans = 4 0 |
octave:4> A = infsup (A);
octave:5> A \ [3; 0] # no solution
ans = 2×1 interval vector
[Empty]
[Empty]
octave:6> A \ [4; 8] # many solutions
ans = 2×1 interval vector
[4]
[Entire]
|
Error handling
Due to the nature of set-based interval arithmetic, you should never observe errors (in the sense of raised GNU Octave error messages) during computation. If you do, there either is a bug in the code or there are unsupported data types.
octave:1> infsup (2, 3) / 0 ans = [Empty] octave:2> infsup (0) ^ infsup (0) ans = [Empty]
However, the interval constructors can produce errors depending on the input. The infsup constructor will fail if the interval boundaries are invalid. Contrariwise, the infsupdec constructor will only issue a warning and return a [NaI], which will propagate and survive through computations.
octave:3> infsup (3, 2) + 1 error: illegal interval boundaries: infimum greater than supremum … (call stack) … octave:3> infsupdec (3, 2) + 1 warning: illegal interval boundaries: infimum greater than supremum ans = [NaI]
Related work
For MATLAB there is a popular interval arithmetic toolbox INTLAB by Siegfried Rump (member of IEEE P1788). It had been free (as in free beer) for academic use in the past, but no longer is. Its origin dates back to 1999, so it is well tested and comprises a lot of functionality, especially for vector / matrix operations. INTLAB is not compatible with GNU Octave. I don't know if INTLAB is or will be compliant with IEEE 1788.
For C++ there is an interval library libIEEE1788 by Marco Nehmeier (member of IEEE P1788). It aims to be standard compliant with IEEE 1788, but is not complete yet.
For Java there is a library jinterval by Dmitry Nadezhin (member of IEEE P1788). It aims to be standard compliant with IEEE 1788, but is not complete yet.