Geometry package: Difference between revisions
No edit summary |
m (Remove redundant Category:Packages.) |
||
| (13 intermediate revisions by 5 users not shown) | |||
| Line 9: | Line 9: | ||
== Tutorials == | == Tutorials == | ||
=== Loading SVG files === | === Loading SVG files === | ||
'''<span style="color:#FF0000;">Coming soon</span>''' | |||
=== Meshing Octave === | === Meshing Octave === | ||
'''<span style="color:#FF0000;">Under construction</span>''' | <!--'''<span style="color:#FF0000;">Under construction</span>''' --> | ||
This tutorial shows the workflow to generate a triangular mesh inside an arbitrary region. | This tutorial shows the workflow to generate a triangular mesh inside an arbitrary region. | ||
| Line 19: | Line 19: | ||
[[File:octave.png|200px|center]] | [[File:octave.png|200px|center]] | ||
<!-- | <!-- {{SyntaxHighlight| --> | ||
{{Code|Loading the file as polygon compatible with geometry package|<syntaxhighlight | {{Code|Loading the file as polygon compatible with geometry package|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
octavesvg = svg ("octave.svg").normalize(); | octavesvg = svg ("octave.svg").normalize(); | ||
ids = octavesvg.pathid(); | ids = octavesvg.pathid(); | ||
| Line 26: | Line 26: | ||
P = bsxfun (@minus, P, centroid (P)); | P = bsxfun (@minus, P, centroid (P)); | ||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
Now we have our SVG as a polygon compatible with the Geometry package format. You can plot the polygon using the function {{Codeline|drawPolygon}}. | Now we have our SVG as a polygon compatible with the Geometry package format. You can plot the polygon using the function {{Codeline|drawPolygon}}. | ||
{{Code|Plotting a polygon compatible with geometry package|< | {{Code|Plotting a polygon compatible with geometry package|<syntaxhighlight lang="matlab" style="font-size:13px"> | ||
drawPolygon (P, "-o"); | drawPolygon (P, "-o"); | ||
</ | </syntaxhighlight>}} | ||
As you can see the polygon has lots of points. We need to simplify the polygon in order to obtain a mesh of reasonable size. Otherwise gmsh will have problems meshing and the result could be huge (or a segmentation fault :( ). The package geometry comes with a simplification function | As you can see the polygon has lots of points. We need to simplify the polygon in order to obtain a mesh of reasonable size. Otherwise gmsh will have problems meshing and the result could be huge (or a segmentation fault :( ). The package geometry (> 1.5.0) comes with a simplification function that uses the [http://en.wikipedia.org/wiki/Ramer%E2%80%93Douglas%E2%80%93Peucker_algorithm Ramer-Douglas-Peucker algorithm] to reduce thenumber of points in the polygon. | ||
{{Code|Symplification of a polygon compatible with geometry package|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
{{Code|Symplification of a polygon compatible with geometry package|< | P = simplifypolygon(P, 'tol', 1e-3); | ||
</syntaxhighlight>}} | |||
You should play with the tolerance option until you get a nice polygon. | |||
</ | |||
The next step is to mesh the interior of the polygon. To do this we could just call {{Codeline|delaunay}} on the polygon and be done with it, but in general such mesh wont be so nice (you will need to add interior points). A very effective way of generating a good mesh is to use the package {{Forge|msh}}, which requires [http://geuz.org/gmsh/ Gmsh] installed in your system. The function {{Codeline|data2geo}} in the Geometry package makes our work very easy: | The next step is to mesh the interior of the polygon. To do this we could just call {{Codeline|delaunay}} on the polygon and be done with it, but in general such mesh wont be so nice (you will need to add interior points). A very effective way of generating a good mesh is to use the package {{Forge|msh}}, which requires [http://geuz.org/gmsh/ Gmsh] installed in your system. The function {{Codeline|data2geo}} in the Geometry package makes our work very easy: | ||
{{Code|Generating mesh for plot with msh package|< | {{Code|Generating mesh for plot with msh package|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load msh | pkg load msh | ||
filename = tmpnam (); | filename = tmpnam (); | ||
| Line 53: | Line 45: | ||
data2geo (P, meshsize, "output", [filename ".geo"]); | data2geo (P, meshsize, "output", [filename ".geo"]); | ||
T = msh2m_gmsh (filename); | T = msh2m_gmsh (filename); | ||
</ | </syntaxhighlight>}} | ||
<!-- </syntaxhighlight> --> | <!-- </syntaxhighlight> --> | ||
After this code finishes, the structure T contains our mesh. To plot the generated mesh we use the function {{Codeline|pdemesh}} from the {{Forge|fpl}} package. In general is a good idea to use the openGL render (called ''fltk'') to plot meshes. | After this code finishes, the structure T contains our mesh. To plot the generated mesh we use the function {{Codeline|pdemesh}} from the {{Forge|fpl}} package. In general is a good idea to use the openGL render (called ''fltk'') to plot meshes. | ||
{{Code|Plotting mesh with fpl package|< | {{Code|Plotting mesh with fpl package|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load fpl | pkg load fpl | ||
graphics_toolkit ('fltk') | graphics_toolkit ('fltk') | ||
| Line 65: | Line 57: | ||
axis tight | axis tight | ||
axis equal | axis equal | ||
</ | </syntaxhighlight>}} | ||
The output should look something like this | The output should look something like this | ||
| Line 78: | Line 70: | ||
* [http://sourceforge.net/apps/mediawiki/matgeom/index.php?title=Main_Page matGeom] | * [http://sourceforge.net/apps/mediawiki/matgeom/index.php?title=Main_Page matGeom] | ||
[[Category: | [[Category:Octave Forge]] | ||
Latest revision as of 11:13, 10 June 2019
The geometry package is multipackage providing functions to manipulate geometrical entities in 2D and 3D. It is based in matGeom and extends it with several other functionalities, e.g. the package provides interfaces with SVG files and polygon meshing using Gmsh.
Relation to matGeom[edit]
octCLIP[edit]
Piece-wise 2D polynomial polygons[edit]
Tutorials[edit]
Loading SVG files[edit]
Coming soon
Meshing Octave[edit]
This tutorial shows the workflow to generate a triangular mesh inside an arbitrary region.
This tutorial requires that you install the package fpl and msh (which requires Gmsh installed in your system). Alternatively, the core function delaunay could be used but the result aren't so pretty.
This tutorial requires an interesting shape to mesh. If you have Inkscape you can create one, and use the previous tutorial to load it into octave. Here I will be using this SVG.
| Code: Loading the file as polygon compatible with geometry package |
octavesvg = svg ("octave.svg").normalize();
ids = octavesvg.pathid();
P = octavesvg.path2polygon (ids{1}, 12)(1:end-1,:);
P = bsxfun (@minus, P, centroid (P));
|
Now we have our SVG as a polygon compatible with the Geometry package format. You can plot the polygon using the function drawPolygon.
| Code: Plotting a polygon compatible with geometry package |
drawPolygon (P, "-o");
|
As you can see the polygon has lots of points. We need to simplify the polygon in order to obtain a mesh of reasonable size. Otherwise gmsh will have problems meshing and the result could be huge (or a segmentation fault :( ). The package geometry (> 1.5.0) comes with a simplification function that uses the Ramer-Douglas-Peucker algorithm to reduce thenumber of points in the polygon.
| Code: Symplification of a polygon compatible with geometry package |
P = simplifypolygon(P, 'tol', 1e-3);
|
You should play with the tolerance option until you get a nice polygon.
The next step is to mesh the interior of the polygon. To do this we could just call delaunay on the polygon and be done with it, but in general such mesh wont be so nice (you will need to add interior points). A very effective way of generating a good mesh is to use the package msh, which requires Gmsh installed in your system. The function data2geo in the Geometry package makes our work very easy:
| Code: Generating mesh for plot with msh package |
pkg load msh
filename = tmpnam ();
meshsize = sqrt (mean (sumsq (diff (P, 1, 1), 2)))/2;
data2geo (P, meshsize, "output", [filename ".geo"]);
T = msh2m_gmsh (filename);
|
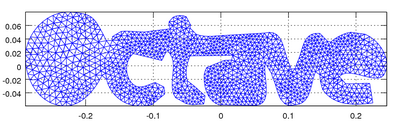
After this code finishes, the structure T contains our mesh. To plot the generated mesh we use the function pdemesh from the fpl package. In general is a good idea to use the openGL render (called fltk) to plot meshes.
| Code: Plotting mesh with fpl package |
pkg load fpl
graphics_toolkit ('fltk')
pdemesh (T.p, T.e, T.t);
view (2)
axis tight
axis equal
|
The output should look something like this
Questions? Ideas? Join us in the mailing list or in the #octave IRC channel.