Fem-fenics: Difference between revisions
No edit summary |
m (Remove redundant Category:Packages.) |
||
| (55 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
Package for solving Partial Differential Equations based on Fenics. | Package for solving Partial Differential Equations based on Fenics. | ||
== Introduction == | |||
'''Fem-Fenics''' is a package for solving partial differential equations. Obviously, Fem-fenics is not the only extra package for Octave with this purpose. For example, [[Bim_package]] uses finite volumes to solve diffusion-advection-reaction equations, while secs1d/2d/3d [http://octave.sourceforge.net/secs1d/index.html] are suited for the resolution of the drift-diffusion system. Furthermore, to use profitably the software, you can integrate it with msh [http://octave.sourceforge.net/msh/index.html] for the generation of the mesh and with fpl [http://octave.sourceforge.net/fpl/index.html] for the post-processing of data. The objective of Fem-fenics is to be a '''generic library of finite elements''', thereby allowing the user to resolve any type of pde, choosing also the most appropriate Finite Element space for any specific problem. | |||
As the name suggests, the Fem-fenics pkg is a wrapper for FEniCS [http://fenicsproject.org/] functions and classes. Thus, ideally the Fem-fenics final goal would be to be able to reproduce all the features available in FEniCS, '''simplifying''' them where it is possible or using the '''Octave function''' whenever available (like the "\" for the resolution of a linear system or the odepkg [http://octave.sourceforge.net/odepkg/index.html] for the resolution of a time dependent problem). | |||
== Tutorials == | == Tutorials == | ||
The solution of a problem can be logically divided in two steps. According to convenience or personal preference, they can be addressed with different files or just in one Octave script: | |||
* the description of the '''abstract problem''': this should be done via the Unified Form Language ('''UFL'''), which is ''a domain specific language for defining discrete variational forms and functionals in a notation '''close to pen-and-paper formulation'''.'' UFL is easy to learn, and in any case the User manual provides explanations and examples. [http://fenicsproject.org/documentation/ufl/1.2.0/user/user_manual.html#ufl-user-manual] As mentioned before, the problem can be defined in a separate .ufl file or handled directly in an m-file using ufl blocks. | |||
* the implementation of a '''specific problem''', an instance of the abstract one: this is done in a script file ('''.m''') where the fem-fenics functions are used and the problem is solved. Their '''syntax is as close as possible to the python interface''', so that Fenics users should be comfortable with it, but it is also quite intuitive for beginners. The examples below show the equivalence between the different programming languages. | |||
=== Poisson Equation === | === Poisson Equation === | ||
Here is a first example for the solution of the Poisson equation. | Here is a first example for the solution of the Poisson equation. | ||
The equation being solved is | The equation being solved is | ||
<math> | <math>-\mathrm{div}\ ( \nabla u(x, y) ) ) = 1 \qquad \mbox{ in } \Omega</math> | ||
<math> u(x, y) = 0 \qquad \mbox{ on } \Gamma_D </math> | <math>u(x, y) = 0 \qquad \mbox{ on } \Gamma_D</math> | ||
<math> ( \nabla u(x, y) ) \cdot \mathbf{n} = 0 \qquad \mbox{ on } \Gamma_N</math> | <math>(\nabla u(x, y) ) \cdot \mathbf{n} = 0 \qquad \mbox{ on } \Gamma_N</math> | ||
A complete description of the problem is avilable on the [http://fenicsproject.org/documentation/dolfin/1.2.0/python/demo/pde/poisson/python/documentation.html Fenics website.] | |||
[[File:Fem-fenics_poisson.png|Location=center]] | |||
<div style="width: 100%;"> | <div style="width: 100%;"> | ||
| Line 16: | Line 33: | ||
{{Code|Define Poisson problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | {{Code|Define Poisson problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load fem-fenics msh | pkg load fem-fenics msh | ||
ufl start Poisson | |||
ufl element = FiniteElement("Lagrange", triangle, 1) | |||
ufl | |||
ufl u = TrialFunction(element) | |||
ufl v = TestFunction(element) | |||
ufl f = Coefficient(element) | |||
ufl g = Coefficient(element) | |||
ufl | |||
ufl a = inner(grad(u), grad(v))*dx | |||
ufl L = f*v*dx + g*v*ds | |||
ufl end | |||
# Create mesh and define function space | # Create mesh and define function space | ||
| Line 22: | Line 50: | ||
mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4)); | mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4)); | ||
V = FunctionSpace('Poisson', mesh); | V = FunctionSpace('Poisson', mesh); | ||
| Line 35: | Line 61: | ||
# Define variational problem | # Define variational problem | ||
# | # Operation performed in the ufl snippet above | ||
# u = TrialFunction(element) | # u = TrialFunction(element) | ||
# v = TestFunction(element) | # v = TestFunction(element) | ||
| Line 45: | Line 71: | ||
g = Expression ('g', @(x,y) sin (5.0 * x)); | g = Expression ('g', @(x,y) sin (5.0 * x)); | ||
# | # As in the ufl snippet above | ||
# a = inner(grad(u), grad(v))*dx | # a = inner(grad(u), grad(v))*dx | ||
# L = f*v*dx + g*v*ds | # L = f*v*dx + g*v*ds | ||
a = BilinearForm ('Poisson', V); | a = BilinearForm ('Poisson', V, V); | ||
L = LinearForm ('Poisson', V, f, g); | L = LinearForm ('Poisson', V, f, g); | ||
| Line 71: | Line 97: | ||
{{Code|Define Poisson problem with fenics python|<syntaxhighlight lang="python" style="font-size:13px"> | {{Code|Define Poisson problem with fenics python|<syntaxhighlight lang="python" style="font-size:13px"> | ||
from dolfin import * | from dolfin import * | ||
| Line 76: | Line 113: | ||
mesh = UnitSquareMesh(32, 32) | mesh = UnitSquareMesh(32, 32) | ||
V = FunctionSpace(mesh, "Lagrange", 1) | V = FunctionSpace(mesh, "Lagrange", 1) | ||
| Line 96: | Line 131: | ||
f = Expression("10*exp(-(pow(x[0] - 0.5, 2) + pow(x[1] - 0.5, 2)) / 0.02)") | f = Expression("10*exp(-(pow(x[0] - 0.5, 2) + | ||
pow(x[1] - 0.5, 2)) / 0.02)") | |||
g = Expression("sin(5*x[0])") | g = Expression("sin(5*x[0])") | ||
| Line 119: | Line 154: | ||
# Plot solution | # Plot solution | ||
plot(u, interactive=True) | plot(u, interactive=True) | ||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
</div> | </div> | ||
| Line 124: | Line 161: | ||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
=== Mixed Formulation for Poisson Equation === | |||
In this example the Poisson equation is solved with a '''mixed approach''': the stable FE space obtained using Brezzi-Douglas-Marini polynomial of order 1 and Discontinuos elements of order 0 is used. | |||
<math>-\mathrm{div}\ ( \mathbf{\sigma} (x, y) ) ) = f (x, y) \qquad \mbox{ in } \Omega</math> | |||
<math> \sigma (x, y) = \nabla u (x, y) \qquad \mbox{ in } \Omega</math> | |||
== | <math>u(x, y) = 0 \qquad \mbox{ on } \Gamma_D</math> | ||
<math>(\sigma (x, y) ) \cdot \mathbf{n} = \sin (5x) \qquad \mbox{ on } \Gamma_N</math> | |||
A complete description of the problem is available on the [http://fenicsproject.org/documentation/dolfin/1.2.0/python/demo/pde/mixed-poisson/python/documentation.html Fenics website.] | |||
<div style="width: 100%;"> | <div style="width: 100%;"> | ||
<div style="float:left; width: 48%"> | <div style="float:left; width: 48%"> | ||
{{Code|Define MixedPoisson problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | {{Code|Define MixedPoisson problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load fem-fenics msh | pkg load fem-fenics msh | ||
ufl start MixedPoisson | |||
ufl | |||
ufl BDM = FiniteElement("BDM", triangle, 1) | |||
ufl DG = FiniteElement("DG", triangle, 0) | |||
ufl W = BDM * DG | |||
ufl | |||
ufl "(sigma, u)" = TrialFunctions(W) | |||
ufl "(tau, v)" = TestFunctions(W) | |||
ufl | |||
ufl CG = FiniteElement("CG", triangle, 1) | |||
ufl f = Coefficient(CG) | |||
ufl | |||
ufl a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx | |||
ufl L = - f*v*dx | |||
ufl end | |||
# Create mesh | # Create mesh | ||
| Line 138: | Line 198: | ||
mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4)); | mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4)); | ||
# | # ufl snippet above | ||
# BDM = FiniteElement("BDM", triangle, 1) | # BDM = FiniteElement("BDM", triangle, 1) | ||
# DG = FiniteElement("DG", triangle, 0) | # DG = FiniteElement("DG", triangle, 0) | ||
| Line 145: | Line 205: | ||
# Define trial and test function | # Define trial and test function | ||
# | # ufl snippet above | ||
# (sigma, u) = TrialFunctions(W) | # (sigma, u) = TrialFunctions(W) | ||
# (tau, v) = TestFunctions(W) | # (tau, v) = TestFunctions(W) | ||
| Line 154: | Line 214: | ||
# Define variational form | # Define variational form | ||
# | # ufl snippet above | ||
# a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx | # a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx | ||
# L = - f*v*dx | # L = - f*v*dx | ||
a = BilinearForm ('MixedPoisson', V); | a = BilinearForm ('MixedPoisson', V, V); | ||
L = LinearForm ('MixedPoisson', V, f); | L = LinearForm ('MixedPoisson', V, f); | ||
| Line 200: | Line 260: | ||
{{Code|Define MixedPoisson problem with fenics python|<syntaxhighlight lang="python" style="font-size:13px"> | {{Code|Define MixedPoisson problem with fenics python|<syntaxhighlight lang="python" style="font-size:13px"> | ||
from dolfin import * | from dolfin import * | ||
# Create mesh | # Create mesh | ||
mesh = UnitSquareMesh(32, 32) | mesh = UnitSquareMesh(32, 32) | ||
| Line 215: | Line 291: | ||
(sigma, u) = TrialFunctions(W) | (sigma, u) = TrialFunctions(W) | ||
(tau, v) = TestFunctions(W) | (tau, v) = TestFunctions(W) | ||
| Line 262: | Line 337: | ||
interactive() | interactive() | ||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
</div> | </div> | ||
| Line 268: | Line 344: | ||
=== Hyperelasticity === | === Hyperelasticity === | ||
This time we compare the code with the | This time we compare the code with the C++ version of DOLFIN. The problem for an elastic material can be expressed as a minimization problem | ||
<math> \min_{u \in V} \Pi</math> | |||
<math> \Pi = \int_{\Omega} \psi(u) \, {\rm d} x - \int_{\Omega} B \cdot u \, {\rm d} x - \int_{\partial\Omega} T \cdot u \, {\rm d} s</math> | |||
where \Pi is the total potential energy, \psi is the elastic stored energy, \B is a body force and \T is a traction force. | |||
A complete description of the problem is avilable on the [http://fenicsproject.org/documentation/dolfin/1.2.0/cpp/demo/pde/hyperelasticity/cpp/documentation.html Fenics website.] The final solution will look like this | |||
[[File:HyperElasticity.png|Location = center|Alignement = center]] | |||
{{Code|HyperElasticity Problem: the ufl file|<syntaxhighlight lang="octave" style="font-size:13px"> | {{Code|HyperElasticity Problem: the ufl file|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
# Function spaces | # Function spaces | ||
| Line 307: | Line 393: | ||
J = derivative(F, u, du) | J = derivative(F, u, du) | ||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
| Line 315: | Line 402: | ||
{{Code|Define HyperElasticity problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | {{Code|Define HyperElasticity problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load fem-fenics msh | pkg load fem-fenics msh | ||
ufl start HyperElasticity | |||
ufl # Function spaces | |||
ufl element = VectorElement("Lagrange", tetrahedron, 1) | |||
ufl | |||
ufl # Trial and test functions | |||
ufl du = TrialFunction(element) # Incremental displacement | |||
ufl v = TestFunction(element) # Test function | |||
ufl | |||
ufl # Functions | |||
ufl u = Coefficient(element) # Displacement from previous iteration | |||
ufl B = Coefficient(element) # Body force per unit volume | |||
ufl T = Coefficient(element) # Traction force on the boundary | |||
ufl | |||
ufl # Kinematics | |||
ufl I = Identity(element.cell().d) # Identity tensor | |||
ufl F = I + grad(u) # Deformation gradient | |||
ufl C = F.T*F # Right Cauchy-Green tensor | |||
ufl | |||
ufl # Invariants of deformation tensors | |||
ufl Ic = tr(C) | |||
ufl J = det(F) | |||
ufl | |||
ufl # Elasticity parameters | |||
ufl mu = Constant(tetrahedron) | |||
ufl lmbda = Constant(tetrahedron) | |||
ufl | |||
ufl # Stored strain energy density (compressible neo-Hookean model) | |||
ufl psi = (mu/2)*(Ic - 3) - mu*ln(J) + (lmbda/2)*(ln(J))**2 | |||
ufl | |||
ufl # Total potential energy | |||
ufl Pi = psi*dx - inner(B, u)*dx - inner(T, u)*ds | |||
ufl | |||
ufl # First variation of Pi (directional derivative about u in the direction of v) | |||
ufl F = derivative(Pi, u, v) | |||
ufl | |||
ufl # Compute Jacobian of F | |||
ufl J = derivative(F, u, du) | |||
ufl end | |||
problem = 'HyperElasticity'; | |||
| Line 428: | Line 554: | ||
u0 = assemble (L, bcs{:}); | u0 = assemble (L, bcs{:}); | ||
# Create function for the resolution of the NL problem | # Create function for the resolution of the NL problem | ||
function [y, jac] = f (problem, xx, V, bc1, bc2, B, T, mu, lmbda) | |||
u = Function ('u', V, xx); | |||
a = JacobianForm (problem, V, mu, lmbda, u); | |||
L = ResidualForm (problem, V, mu, lmbda, B, T, u); | |||
if (nargout == 1) | |||
[y, xx] = assemble (L, xx, bc1, bc2); | |||
elseif (nargout == 2) | |||
[jac, y, xx] = assemble_system (a, L, xx, bc1, bc2); | |||
endif | |||
endfunction | |||
fs = @(xx) f (problem, xx, V, bcl, bcr, B, T, mu, lmbda); | fs = @(xx) f (problem, xx, V, bcl, bcr, B, T, mu, lmbda); | ||
[x, fval, info] = fsolve (fs, u0, optimset ("jacobian", "on")); | [x, fval, info] = fsolve (fs, u0, optimset ("jacobian", "on")); | ||
| Line 459: | Line 586: | ||
using namespace dolfin; | using namespace dolfin; | ||
// Sub domain for clamp at left end | // Sub domain for clamp at left end | ||
| Line 513: | Line 679: | ||
// New coordinates | // New coordinates | ||
double y = y0 + (x[1] - y0)*cos(theta) - (x[2] - z0)*sin(theta); | double y = y0 + (x[1]-y0)*cos(theta) - (x[2]-z0)*sin(theta); | ||
double z = z0 + (x[1] - y0)*sin(theta) + (x[2] - z0)*cos(theta); | double z = z0 + (x[1]-y0)*sin(theta) + (x[2]-z0)*cos(theta); | ||
// Rotate at right end | // Rotate at right end | ||
| Line 568: | Line 734: | ||
// Solve nonlinear variational problem F(u; v) = 0 | // Solve nonlinear variational problem F(u; v) = 0 | ||
solve(F == 0, u, bcs, J); | solve(F == 0, u, bcs, J); | ||
| Line 593: | Line 760: | ||
return 0; | return 0; | ||
} | } | ||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | |||
</div> | |||
</div> | |||
<div style="clear:both"></div> | |||
=== Incompressible Navier-Stokes equations === | |||
The incompressible Navier-Stokes equations are solved using the Chorin-Temam projection algorithm. [http://en.wikipedia.org/wiki/Projection_method_%28fluid_dynamics%29#Chorin.27s_projection_method]. | |||
A complete description of the specific problem is avilable on the [http://fenicsproject.org/documentation/dolfin/1.2.0/python/demo/pde/navier-stokes/python/documentation.html Fenics website.] | |||
<div style="width: 100%;"> | |||
<div style="float:left; width: 48%"> | |||
{{Code|Define HyperElasticity problem with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
pkg load fem-fenics msh | |||
import_ufl_Problem ("TentativeVelocity"); | |||
import_ufl_Problem ("VelocityUpdate"); | |||
import_ufl_Problem ("PressureUpdate"); | |||
# We can either load the mesh from the file as in Dolfin but | |||
# we can also use the msh pkg to generate the L-shape domain | |||
name = [tmpnam ".geo"]; | |||
fid = fopen (name, "w"); | |||
fputs (fid,"Point (1) = {0, 0, 0, 0.1};\n"); | |||
fputs (fid,"Point (2) = {1, 0, 0, 0.1};\n"); | |||
fputs (fid,"Point (3) = {1, 0.5, 0, 0.1};\n"); | |||
fputs (fid,"Point (4) = {0.5, 0.5, 0, 0.1};\n"); | |||
fputs (fid,"Point (5) = {0.5, 1, 0, 0.1};\n"); | |||
fputs (fid,"Point (6) = {0, 1, 0,0.1};\n"); | |||
fputs (fid,"Line (1) = {5, 6};\n"); | |||
fputs (fid,"Line (2) = {2, 3};\n"); | |||
fputs (fid,"Line(3) = {6,1,2};\n"); | |||
fputs (fid,"Line(4) = {5,4,3};\n"); | |||
fputs (fid,"Line Loop(7) = {3,2,-4,1};\n"); | |||
fputs (fid,"Plane Surface(8) = {7};\n"); | |||
fclose (fid); | |||
msho = msh2m_gmsh (canonicalize_file_name (name)(1:end-4),... | |||
"scale", 1,"clscale", .2); | |||
unlink (canonicalize_file_name (name)); | |||
mesh = Mesh (msho); | |||
# Define function spaces (P2-P1). From ufl file | |||
# V = VectorElement("CG", triangle, 2) | |||
# Q = FiniteElement("CG", triangle, 1) | |||
V = FunctionSpace ('VelocityUpdate', mesh); | |||
Q = FunctionSpace ('PressureUpdate', mesh); | |||
# Define trial and test functions. From ufl file | |||
# u = TrialFunction(V) | |||
# p = TrialFunction(Q) | |||
# v = TestFunction(V) | |||
# q = TestFunction(Q) | |||
# Set parameter values. From ufl file | |||
# nu = 0.01 | |||
dt = 0.01; | |||
T = 3.; | |||
# Define boundary conditions | |||
noslip = DirichletBC (V, @(x,y) [0; 0], [3, 4]); | |||
outflow = DirichletBC (Q, @(x,y) 0, 2); | |||
# Create functions | |||
u0 = Expression ('u0', @(x,y) [0; 0]); | |||
# Define coefficients | |||
k = Constant ('k', dt); | |||
f = Constant ('f', [0; 0]); | |||
# Tentative velocity step. From ufl file | |||
# eq = (1/k)*inner(u - u0, v)*dx + inner(grad(u0)*u0, v)*dx \ | |||
# + nu*inner(grad(u), grad(v))*dx - inner(f, v)*dx | |||
a1 = BilinearForm ('TentativeVelocity', V, V, k); | |||
# Pressure update. From ufl file | |||
# a = inner(grad(p), grad(q))*dx | |||
# L = -(1/k)*div(u1)*q*dx | |||
a2 = BilinearForm ('PressureUpdate', Q, Q); | |||
# Velocity update | |||
# a = inner(u, v)*dx | |||
# L = inner(u1, v)*dx - k*inner(grad(p1), v)*dx | |||
a3 = BilinearForm ('VelocityUpdate', V, V); | |||
# Assemble matrices | |||
A1 = assemble (a1, noslip); | |||
A3 = assemble (a3, noslip); | |||
# Time-stepping | |||
t = dt; i = 0; | |||
while t < T | |||
# Update pressure boundary condition | |||
inflow = DirichletBC (Q, @(x,y) sin(3.0*t), 1); | |||
# Compute tentative velocity step | |||
"Computing tentative velocity" | |||
L1 = LinearForm ('TentativeVelocity', V, k, u0, f); | |||
b1 = assemble (L1, noslip); | |||
utmp = A1 \ b1; | |||
u1 = Function ('u1', V, utmp); | |||
# Pressure correction | |||
"Computing pressure correction" | |||
L2 = LinearForm ('PressureUpdate', Q, u1, k); | |||
[A2, b2] = assemble_system (a2, L2, inflow, outflow); | |||
ptmp = A2 \ b2; | |||
p1 = Function ('p1', Q, ptmp); | |||
# Velocity correction | |||
"Computing velocity correction" | |||
L3 = LinearForm ('VelocityUpdate', V, k, u1, p1); | |||
b3 = assemble (L3, noslip); | |||
ut = A3 \ b3; | |||
u1 = Function ('u0', V, ut); | |||
# Plot solution | |||
plot (p1); | |||
plot (u1); | |||
# Save to file | |||
save (p1, sprintf ("p_%3.3d", ++i)); | |||
save (u1, sprintf ("u_%3.3d", i)); | |||
# Move to next time step | |||
u0 = u1; | |||
t += dt | |||
end | |||
</syntaxhighlight>}} | |||
</div> | |||
<div style="float:right; width: 48%"> | |||
{{Code|Define NS problem with fenics python |<syntaxhighlight lang="python" style="font-size:13px"> | |||
from dolfin import * | |||
# Load mesh from file | |||
mesh = Mesh("lshape.xml.gz") | |||
# Define function spaces (P2-P1) | |||
V = VectorFunctionSpace(mesh, "CG", 2) | |||
Q = FunctionSpace(mesh, "CG", 1) | |||
# Define trial and test functions | |||
u = TrialFunction(V) | |||
p = TrialFunction(Q) | |||
v = TestFunction(V) | |||
q = TestFunction(Q) | |||
# Set parameter values | |||
dt = 0.01 | |||
T = 3 | |||
nu = 0.01 | |||
# Define time-dependent pressure boundary condition | |||
p_in = Expression("sin(3.0*t)", t=0.0) | |||
# Define boundary conditions | |||
noslip = DirichletBC(V, (0, 0), | |||
"on_boundary && \ | |||
(x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \ | |||
(x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))") | |||
inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS") | |||
outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS") | |||
bcu = [noslip] | |||
bcp = [inflow, outflow] | |||
# Create functions | |||
u0 = Function(V) | |||
u1 = Function(V) | |||
p1 = Function(Q) | |||
# Define coefficients | |||
k = Constant(dt) | |||
f = Constant((0, 0)) | |||
# Tentative velocity step | |||
F1 = (1/k)*inner(u - u0, v)*dx + inner(grad(u0)*u0, v)*dx \ | |||
+ nu*inner(grad(u), grad(v))*dx - inner(f, v)*dx | |||
a1 = lhs(F1) | |||
L1 = rhs(F1) | |||
# Pressure update | |||
a2 = inner(grad(p), grad(q))*dx | |||
L2 = -(1/k)*div(u1)*q*dx | |||
# Velocity update | |||
a3 = inner(u, v)*dx | |||
L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx | |||
# Assemble matrices | |||
A1 = assemble(a1) | |||
A2 = assemble(a2) | |||
A3 = assemble(a3) | |||
# Use amg preconditioner if available | |||
prec = "amg" if has_krylov_solver_preconditioner("amg") | |||
else "default" | |||
# Create files for storing solution | |||
ufile = File("results/velocity.pvd") | |||
pfile = File("results/pressure.pvd") | |||
# Time-stepping | |||
t = dt | |||
while t < T + DOLFIN_EPS: | |||
# Update pressure boundary condition | |||
p_in.t = t | |||
# Compute tentative velocity step | |||
begin("Computing tentative velocity") | |||
b1 = assemble(L1) | |||
[bc.apply(A1, b1) for bc in bcu] | |||
solve(A1, u1.vector(), b1, "gmres", "default") | |||
end() | |||
# Pressure correction | |||
begin("Computing pressure correction") | |||
b2 = assemble(L2) | |||
[bc.apply(A2, b2) for bc in bcp] | |||
solve(A2, p1.vector(), b2, "gmres", prec) | |||
end() | |||
# Velocity correction | |||
begin("Computing velocity correction") | |||
b3 = assemble(L3) | |||
[bc.apply(A3, b3) for bc in bcu] | |||
solve(A3, u1.vector(), b3, "gmres", "default") | |||
end() | |||
# Plot solution | |||
plot(p1, title="Pressure", rescale=True) | |||
plot(u1, title="Velocity", rescale=True) | |||
# Save to file | |||
ufile << u1 | |||
pfile << p1 | |||
# Move to next time step | |||
u0.assign(u1) | |||
t += dt | |||
print "t =", t | |||
# Hold plot | |||
interactive() | |||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | </syntaxhighlight>}} | ||
</div> | </div> | ||
</div> | </div> | ||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
[[ | |||
[[Category: | === Obstacles in the Domain === | ||
[[File:Fem_fenics_Subdomains.png|right|500px]] | |||
<math> - \mathrm {div} (a \nabla u) = 1 \quad \mbox { in } \Omega, </math> | |||
<math> u = 5 \quad \mbox { on } \Gamma_T, </math> | |||
<math> u = 0 \quad \mbox { on } \Gamma_B, </math> | |||
<math> \nabla u \cdot \mathbf {n} = - 10 e^{- (y - 0.5)^2} \quad \mbox { on } \Gamma_L, </math> | |||
<math> \nabla u \cdot \mathbf {n} = 1 \quad \mbox { on } \Gamma_R </math> | |||
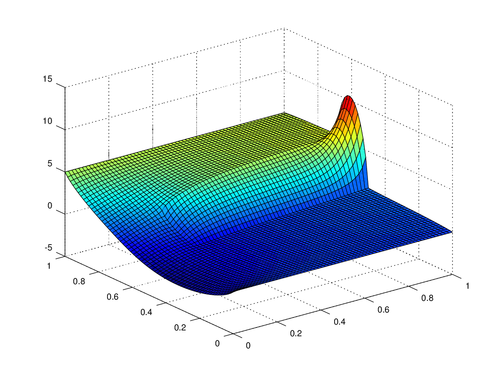
The above example is a weighted Poisson problem on the unit square. The diffusion coefficient <math> a </math> assumes value 0.01 on the obstacle <math> \Omega_1 = [0.5, 0.7] \times [0.2, 1.0] </math>, whilst 1 outside on <math> \Omega_0 = \Omega \setminus \Omega_1 </math>. You can find a detailed explanation on the [http://fenicsproject.org/documentation/dolfin/1.4.0/python/demo/documented/subdomains-poisson/python/documentation.html FEniCS website]. On the side, you can see the solution. | |||
<div style="clear: both"></div> | |||
<div style="width: 100%;"> | |||
<div style="float:left; width: 48%"> | |||
{{Code|Define Poisson problem with obstacle with fem-fenics|<syntaxhighlight lang="octave" style="font-size:13px"> | |||
pkg load fem-fenics msh | |||
# Create mesh | |||
x = y = linspace (0, 1, 65); | |||
[msh, facets] = Mesh (msh2m_structured_mesh (x, y, 0, 4:-1:1)); | |||
ufl start Subdomains | |||
ufl fe = FiniteElement "(""CG"", triangle, 2)" | |||
ufl u = TrialFunction (fe) | |||
ufl v = TestFunction (fe) | |||
ufl | |||
ufl a0 = Coefficient (fe) | |||
ufl a1 = Coefficient (fe) | |||
ufl g_L = Coefficient (fe) | |||
ufl g_R = Coefficient (fe) | |||
ufl f = Coefficient (fe) | |||
ufl | |||
ufl a= "inner(a0*grad(u),grad(v))*dx(0) + inner(a1*grad(u),grad(v))*dx(1)" | |||
ufl L = g_L*v*ds(1) + g_R*v*ds(3) + f*v*dx(0) + f*v*dx(1) | |||
ufl end | |||
V = FunctionSpace ("Subdomains", msh); | |||
# Define problem coefficients | |||
a0 = Constant ("a0", 1.0); | |||
a1 = Constant ("a1", 0.01); | |||
g_L = Expression ("g_L", @(x, y) - 10*exp(- (y - 0.5) ^ 2)); | |||
g_R = Constant ("g_R", 1.0); | |||
f = Constant ("f", 1.0); | |||
# Define subdomains | |||
domains = MeshFunction ("dx", msh, 2, 0); | |||
obstacle = SubDomain (@(x,y) (y >= 0.5) && (y <= 0.7) && ... | |||
(x >= 0.2) && (x <= 1.0), false); | |||
domains = mark (obstacle, domains, 1); | |||
# Define boundary conditions | |||
bc1 = DirichletBC (V, @(x, y) 5.0, facets, 2); | |||
bc2 = DirichletBC (V, @(x, y) 0.0, facets, 4); | |||
# Define variational form | |||
a = BilinearForm ("Subdomains", V, V, a0, a1, domains); | |||
L = LinearForm ("Subdomains", V, g_L, g_R, f, facets, domains); | |||
# Solve problem | |||
[A, b] = assemble_system (a, L, bc1, bc2); | |||
sol = A \ b; | |||
u = Function ("u", V, sol); | |||
# Plot solution | |||
[X, Y] = meshgrid (x, y); | |||
U = u (X, Y); | |||
surf (X, Y, U); | |||
</syntaxhighlight>}} | |||
</div> | |||
<div style="float:right; width: 48%"> | |||
{{Code|Define Poisson problem with obstacle with FEniCS python |<syntaxhighlight lang="python" style="font-size:13px"> | |||
from dolfin import * | |||
# Define mesh | |||
mesh = UnitSquareMesh(64, 64) | |||
# Create classes for defining parts of the boundaries | |||
class Left(SubDomain): | |||
def inside(self, x, on_boundary): | |||
return near(x[0], 0.0) | |||
class Right(SubDomain): | |||
def inside(self, x, on_boundary): | |||
return near(x[0], 1.0) | |||
class Bottom(SubDomain): | |||
def inside(self, x, on_boundary): | |||
return near(x[1], 0.0) | |||
class Top(SubDomain): | |||
def inside(self, x, on_boundary): | |||
return near(x[1], 1.0) | |||
# Initialize sub-domain instances | |||
left = Left() | |||
top = Top() | |||
right = Right() | |||
bottom = Bottom() | |||
# Initialize mesh function for boundary domains | |||
boundaries = FacetFunction("size_t", mesh) | |||
boundaries.set_all(0) | |||
left.mark(boundaries, 1) | |||
top.mark(boundaries, 2) | |||
right.mark(boundaries, 3) | |||
bottom.mark(boundaries, 4) | |||
# Define function space and basis functions | |||
V = FunctionSpace(mesh, "CG", 2) | |||
u = TrialFunction(V) | |||
v = TestFunction(V) | |||
# Define input data | |||
a0 = Constant(1.0) | |||
a1 = Constant(0.01) | |||
g_L = Expression("- 10*exp(- pow(x[1] - 0.5, 2))") | |||
g_R = Constant("1.0") | |||
f = Constant(1.0) | |||
# Initialize mesh function for interior domains | |||
class Obstacle(SubDomain): | |||
def inside(self, x, on_boundary): | |||
return (between(x[1], (0.5, 0.7)) and between(x[0], (0.2, 1.0))) | |||
obstacle = Obstacle() | |||
domains = CellFunction("size_t", mesh) | |||
domains.set_all(0) | |||
obstacle.mark(domains, 1) | |||
# Define Dirichlet boundary conditions at top and bottom boundaries | |||
bcs = [DirichletBC(V, 5.0, boundaries, 2), | |||
DirichletBC(V, 0.0, boundaries, 4)] | |||
# Define new measures associated with the interior domains and | |||
# exterior boundaries | |||
dx = Measure("dx")[domains] | |||
ds = Measure("ds")[boundaries] | |||
# Define variational form | |||
F = (inner(a0*grad(u), grad(v))*dx(0) + inner(a1*grad(u), grad(v))*dx(1) | |||
- g_L*v*ds(1) - g_R*v*ds(3) | |||
- f*v*dx(0) - f*v*dx(1)) | |||
# Separate left and right hand sides of equation | |||
a, L = lhs(F), rhs(F) | |||
# Solve problem | |||
u = Function(V) | |||
solve(a == L, u, bcs) | |||
# Plot solution | |||
plot(u, title="u") | |||
interactive() | |||
© Copyright 2011, The FEniCS Project | |||
</syntaxhighlight>}} | |||
</div> | |||
</div> | |||
<div style="clear:both"></div> | |||
== Relevant Implementation Details == | |||
The relevant implementation details which the user should know are: | |||
* All the objects are managed using boost::shared_ptr <>. It means that '''the same resource can be shared by more objects''' and useless copies should be avoided. For example, if we have two different functional spaces in the same problem, like with Navier-Stokes for the velocity and the pressure, the mesh is shared between them and no one has its own copy. | |||
* The '''essential BC are imposed directly to the matrix''' with the command '''assemble()''', which sets to zero all the off diagonal elements in the corresponding line, sets to 1 the diagonal element and sets to the exact value the rhs. This means that we could loose the symmetry of the matrix, if any. To avoid this problem and preserve the symmetry of the system it is available the '''assemble_system()''' command which builds at once the lhs and the rhs. | |||
* The '''coefficient of the variational problem''' can be specified using either an ''Expression()'', a ''Constant()'' or a ''Function()''. They are different objects which behave in different ways: an ''Expression'' or a ''Constant'' object overloads the eval() method of the dolfin::Expression class and it is evaluated at run time using the octave function feval (). A ''Function'' instead doesn't need to be evaluated because it is assembled copying element-by-element the values contained in the input vector. | |||
* Unfortunately the feature used in previous versions of the package to handle ''DirichletBC'' is not implemented yet in the FEniCS library for distributed execution. This means that prior to running code via MPI it should be adapted to use the newly introduced ''MeshFunction'' to mark border subsets, so that essential boundary conditions are correctly applied. | |||
== Known issues == | |||
* Fem-fenics needs both in the installation phase and in normal usage some includes that are not in standard system include directories, namely those related to MPI and the Eigen template library. If you experience an installation failure or errors when importing your UFL files, then you should properly set your CPPFLAGS environment variable before launching Octave, as per [http://octave.1599824.n4.nabble.com/fem-fenics-0-0-1-released-tp4662182p4662195.html]. This can be done in {{Path|sh}} compatible shells with the command below: | |||
<syntaxhighlight lang="bash" style="font-size:13px"> | |||
export CPPFLAGS="-I/usr/include/eigen3 $(mpicxx -showme:compile)" | |||
</syntaxhighlight> | |||
Notice that {{Path|/usr/include/eigen3}} has to be changed accordingly to the path in which Eigen are to be found on your system. | |||
It should readily work in Ubuntu 13.10 and 14.04. | |||
* There is a known bug with Openmpi, discussed on the maintainers list [http://octave.1599824.n4.nabble.com/fem-fenics-0-0-1-released-tp4662182p4662234.html], that needs the preloading of a MPI shared library with the following command: | |||
<syntaxhighlight lang="bash" style="font-size:13px"> | |||
export LD_PRELOAD=/usr/lib/openmpi/lib/libmpi.so | |||
</syntaxhighlight> | |||
Again, notice that {{Path|/usr/lib/openmpi/lib/libmpi.so}} has to be changed to fit to your system. | |||
== Additional functionality / TODOS == | |||
Obviously, Fem-fenics is not (yet) able to reproduce all the functionality available in Fenics. If there is any important features missing, please add it to the list below. (Or, better, you can directly submit your extension to the mercurial repository [https://sourceforge.net/p/octave/fem-fenics/ci/default/tree/]). | |||
* '''Norma'''l: add the possibility to use a reserved keyword (normal ?) to be used with the DirichletBC. <syntaxhighlight lang="octave" style="font-size:13px"> bc = DirichletBC (V, @(x, y, normal) [sin(x)*normal; 0], [3, 4]);</syntaxhighlight> | |||
* <strike> @function/'''feval''': the function should accept as input also an array of values. </strike> Show how it can be used in an example with odepkg. | |||
== External Links == | |||
* User manual [https://drive.google.com/file/d/0ByWLfuWVSWHbaXN3T3diaXEwU0k/edit?usp=sharing]. | |||
* Repository [http://sourceforge.net/p/octave/fem-fenics/] | |||
* Functions reference [http://octave.sourceforge.net/fem-fenics/overview.html] | |||
* Presentation at MOX [https://drive.google.com/file/d/0ByWLfuWVSWHbZWZzRzY2em5PU28/edit?usp=sharing] | |||
[[Category:Octave Forge]] | |||
Latest revision as of 11:12, 10 June 2019
Package for solving Partial Differential Equations based on Fenics.
Introduction[edit]
Fem-Fenics is a package for solving partial differential equations. Obviously, Fem-fenics is not the only extra package for Octave with this purpose. For example, Bim_package uses finite volumes to solve diffusion-advection-reaction equations, while secs1d/2d/3d [1] are suited for the resolution of the drift-diffusion system. Furthermore, to use profitably the software, you can integrate it with msh [2] for the generation of the mesh and with fpl [3] for the post-processing of data. The objective of Fem-fenics is to be a generic library of finite elements, thereby allowing the user to resolve any type of pde, choosing also the most appropriate Finite Element space for any specific problem.
As the name suggests, the Fem-fenics pkg is a wrapper for FEniCS [4] functions and classes. Thus, ideally the Fem-fenics final goal would be to be able to reproduce all the features available in FEniCS, simplifying them where it is possible or using the Octave function whenever available (like the "\" for the resolution of a linear system or the odepkg [5] for the resolution of a time dependent problem).
Tutorials[edit]
The solution of a problem can be logically divided in two steps. According to convenience or personal preference, they can be addressed with different files or just in one Octave script:
- the description of the abstract problem: this should be done via the Unified Form Language (UFL), which is a domain specific language for defining discrete variational forms and functionals in a notation close to pen-and-paper formulation. UFL is easy to learn, and in any case the User manual provides explanations and examples. [6] As mentioned before, the problem can be defined in a separate .ufl file or handled directly in an m-file using ufl blocks.
- the implementation of a specific problem, an instance of the abstract one: this is done in a script file (.m) where the fem-fenics functions are used and the problem is solved. Their syntax is as close as possible to the python interface, so that Fenics users should be comfortable with it, but it is also quite intuitive for beginners. The examples below show the equivalence between the different programming languages.
Poisson Equation[edit]
Here is a first example for the solution of the Poisson equation. The equation being solved is
A complete description of the problem is avilable on the Fenics website.
| Code: Define Poisson problem with fem-fenics |
pkg load fem-fenics msh
ufl start Poisson
ufl element = FiniteElement("Lagrange", triangle, 1)
ufl
ufl u = TrialFunction(element)
ufl v = TestFunction(element)
ufl f = Coefficient(element)
ufl g = Coefficient(element)
ufl
ufl a = inner(grad(u), grad(v))*dx
ufl L = f*v*dx + g*v*ds
ufl end
# Create mesh and define function space
x = y = linspace (0, 1, 33);
mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4));
V = FunctionSpace('Poisson', mesh);
# Define boundary condition
bc = DirichletBC(V, @(x, y) 0.0, [2;4]);
# Define variational problem
# Operation performed in the ufl snippet above
# u = TrialFunction(element)
# v = TestFunction(element)
# f = Coefficient(element)
# g = Coefficient(element)
f = Expression ('f',
@(x,y) 10*exp(-((x - 0.5)^2 + (y - 0.5)^2) / 0.02));
g = Expression ('g', @(x,y) sin (5.0 * x));
# As in the ufl snippet above
# a = inner(grad(u), grad(v))*dx
# L = f*v*dx + g*v*ds
a = BilinearForm ('Poisson', V, V);
L = LinearForm ('Poisson', V, f, g);
# Compute solution
[A, b] = assemble_system (a, L, bc);
sol = A \ b;
u = Function ('u', V, sol);
# Save solution in VTK format
save (u, 'poisson')
# Plot solution
plot (u);
|
| Code: Define Poisson problem with fenics python |
from dolfin import *
# Create mesh and define function space
mesh = UnitSquareMesh(32, 32)
V = FunctionSpace(mesh, "Lagrange", 1)
# Define Dirichlet boundary (x = 0 or x = 1)
def boundary(x):
return x[0] < DOLFIN_EPS or x[0] > 1.0 - DOLFIN_EPS
# Define boundary condition
u0 = Constant(0.0)
bc = DirichletBC(V, u0, boundary)
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Expression("10*exp(-(pow(x[0] - 0.5, 2) +
pow(x[1] - 0.5, 2)) / 0.02)")
g = Expression("sin(5*x[0])")
a = inner(grad(u), grad(v))*dx
L = f*v*dx + g*v*ds
# Compute solution
u = Function(V)
(A, b) = assemble_system (a, L, bc);
solve(A, u.vector(), b, "gmres", "default")
# Save solution in VTK format
file = File("poisson.pvd")
file << u
# Plot solution
plot(u, interactive=True)
© Copyright 2011, The FEniCS Project
|
Mixed Formulation for Poisson Equation[edit]
In this example the Poisson equation is solved with a mixed approach: the stable FE space obtained using Brezzi-Douglas-Marini polynomial of order 1 and Discontinuos elements of order 0 is used.
A complete description of the problem is available on the Fenics website.
| Code: Define MixedPoisson problem with fem-fenics |
pkg load fem-fenics msh
ufl start MixedPoisson
ufl
ufl BDM = FiniteElement("BDM", triangle, 1)
ufl DG = FiniteElement("DG", triangle, 0)
ufl W = BDM * DG
ufl
ufl "(sigma, u)" = TrialFunctions(W)
ufl "(tau, v)" = TestFunctions(W)
ufl
ufl CG = FiniteElement("CG", triangle, 1)
ufl f = Coefficient(CG)
ufl
ufl a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx
ufl L = - f*v*dx
ufl end
# Create mesh
x = y = linspace (0, 1, 33);
mesh = Mesh(msh2m_structured_mesh (x, y, 1, 1:4));
# ufl snippet above
# BDM = FiniteElement("BDM", triangle, 1)
# DG = FiniteElement("DG", triangle, 0)
# W = BDM * DG
V = FunctionSpace('MixedPoisson', mesh);
# Define trial and test function
# ufl snippet above
# (sigma, u) = TrialFunctions(W)
# (tau, v) = TestFunctions(W)
# CG = FiniteElement("CG", triangle, 1)
# f = Coefficient(CG)
f = Expression ('f',
@(x,y) 10*exp(-((x - 0.5)^2 + (y - 0.5)^2) / 0.02));
# Define variational form
# ufl snippet above
# a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx
# L = - f*v*dx
a = BilinearForm ('MixedPoisson', V, V);
L = LinearForm ('MixedPoisson', V, f);
# Define essential boundary
bc1 = DirichletBC (SubSpace (V, 1), @(x,y) [0; -sin(5.0*x)], 1);
bc2 = DirichletBC (SubSpace (V, 1), @(x,y) [0; sin(5.0*x)], 3);
# Compute solution
[A, b] = assemble_system (a, L, bc1, bc2);
sol = A \ b;
func = Function ('func', V, sol);
sigma = Function ('sigma', func, 1);
u = Function ('u', func, 2);
# Plot solution
plot (sigma);
plot (u);
|
| Code: Define MixedPoisson problem with fenics python |
from dolfin import *
# Create mesh
mesh = UnitSquareMesh(32, 32)
# Define function spaces and mixed (product) space
BDM = FunctionSpace(mesh, "BDM", 1)
DG = FunctionSpace(mesh, "DG", 0)
W = BDM * DG
# Define trial and test functions
(sigma, u) = TrialFunctions(W)
(tau, v) = TestFunctions(W)
f = Expression
("10*exp(-(pow(x[0] - 0.5, 2) + pow(x[1] - 0.5, 2)) / 0.02)")
# Define variational form
a = (dot(sigma, tau) + div(tau)*u + div(sigma)*v)*dx
L = - f*v*dx
# Define function G such that G \cdot n = g
class BoundarySource(Expression):
def __init__(self, mesh):
self.mesh = mesh
def eval_cell(self, values, x, ufc_cell):
cell = Cell(self.mesh, ufc_cell.index)
n = cell.normal(ufc_cell.local_facet)
g = sin(5*x[0])
values[0] = g*n[0]
values[1] = g*n[1]
def value_shape(self):
return (2,)
G = BoundarySource(mesh)
# Define essential boundary
def boundary(x):
return x[1] < DOLFIN_EPS or x[1] > 1.0 - DOLFIN_EPS
bc = DirichletBC(W.sub(0), G, boundary)
# Compute solution
w = Function(W)
solve(a == L, w, bc)
(sigma, u) = w.split()
# Plot sigma and u
plot(sigma)
plot(u)
interactive()
© Copyright 2011, The FEniCS Project
|
Hyperelasticity[edit]
This time we compare the code with the C++ version of DOLFIN. The problem for an elastic material can be expressed as a minimization problem
where \Pi is the total potential energy, \psi is the elastic stored energy, \B is a body force and \T is a traction force.
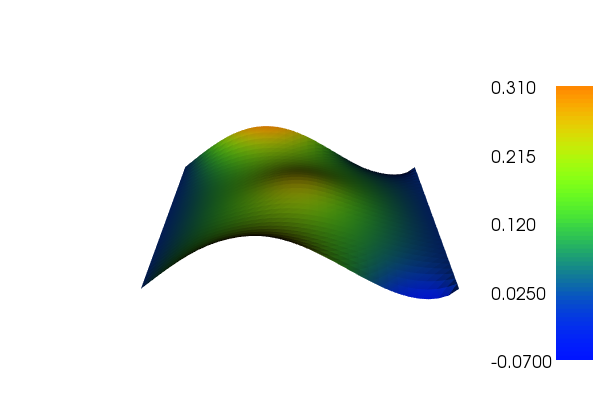
A complete description of the problem is avilable on the Fenics website. The final solution will look like this

| Code: HyperElasticity Problem: the ufl file |
# Function spaces
element = VectorElement("Lagrange", tetrahedron, 1)
# Trial and test functions
du = TrialFunction(element) # Incremental displacement
v = TestFunction(element) # Test function
# Functions
u = Coefficient(element) # Displacement from previous iteration
B = Coefficient(element) # Body force per unit volume
T = Coefficient(element) # Traction force on the boundary
# Kinematics
I = Identity(element.cell().d) # Identity tensor
F = I + grad(u) # Deformation gradient
C = F.T*F # Right Cauchy-Green tensor
# Invariants of deformation tensors
Ic = tr(C)
J = det(F)
# Elasticity parameters
mu = Constant(tetrahedron)
lmbda = Constant(tetrahedron)
# Stored strain energy density (compressible neo-Hookean model)
psi = (mu/2)*(Ic - 3) - mu*ln(J) + (lmbda/2)*(ln(J))**2
# Total potential energy
Pi = psi*dx - inner(B, u)*dx - inner(T, u)*ds
# First variation of Pi (directional derivative about u in the direction of v)
F = derivative(Pi, u, v)
# Compute Jacobian of F
J = derivative(F, u, du)
© Copyright 2011, The FEniCS Project
|
| Code: Define HyperElasticity problem with fem-fenics |
pkg load fem-fenics msh
ufl start HyperElasticity
ufl # Function spaces
ufl element = VectorElement("Lagrange", tetrahedron, 1)
ufl
ufl # Trial and test functions
ufl du = TrialFunction(element) # Incremental displacement
ufl v = TestFunction(element) # Test function
ufl
ufl # Functions
ufl u = Coefficient(element) # Displacement from previous iteration
ufl B = Coefficient(element) # Body force per unit volume
ufl T = Coefficient(element) # Traction force on the boundary
ufl
ufl # Kinematics
ufl I = Identity(element.cell().d) # Identity tensor
ufl F = I + grad(u) # Deformation gradient
ufl C = F.T*F # Right Cauchy-Green tensor
ufl
ufl # Invariants of deformation tensors
ufl Ic = tr(C)
ufl J = det(F)
ufl
ufl # Elasticity parameters
ufl mu = Constant(tetrahedron)
ufl lmbda = Constant(tetrahedron)
ufl
ufl # Stored strain energy density (compressible neo-Hookean model)
ufl psi = (mu/2)*(Ic - 3) - mu*ln(J) + (lmbda/2)*(ln(J))**2
ufl
ufl # Total potential energy
ufl Pi = psi*dx - inner(B, u)*dx - inner(T, u)*ds
ufl
ufl # First variation of Pi (directional derivative about u in the direction of v)
ufl F = derivative(Pi, u, v)
ufl
ufl # Compute Jacobian of F
ufl J = derivative(F, u, du)
ufl end
problem = 'HyperElasticity';
Rotation = @(x,y,z) ...
[0; ...
0.5*(0.5 + (y - 0.5)*cos(pi/3) - (z-0.5)*sin(pi/3) - y);...
0.5*(0.5 + (y - 0.5)*sin(pi/3) + (z-0.5)*cos(pi/3) - z)];
#Create mesh and define function space
x = y = z = linspace (0, 1, 17);
mshd = Mesh (msh3m_structured_mesh (x, y, z, 1, 1:6));
V = FunctionSpace (problem, mshd);
# Create Dirichlet boundary conditions
bcl = DirichletBC (V, @(x,y,z) [0; 0; 0], 1);
bcr = DirichletBC (V, Rotation, 2);
bcs = {bcl, bcr};
# Define source and boundary traction functions
B = Constant ('B', [0.0; -0.5; 0.0]);
T = Constant ('T', [0.1; 0.0; 0.0]);
# Set material parameters
E = 10.0;
nu = 0.3;
mu = Constant ('mu', E./(2*(1+nu)));
lmbda = Constant ('lmbda', E*nu./((1+nu)*(1-2*nu)));
u = Expression ('u', @(x,y,z) [0; 0; 0]);
# Create (linear) form defining (nonlinear) variational problem
L = ResidualForm (problem, V, mu, lmbda, B, T, u);
# Solve nonlinear variational problem F(u; v) = 0
u0 = assemble (L, bcs{:});
# Create function for the resolution of the NL problem
function [y, jac] = f (problem, xx, V, bc1, bc2, B, T, mu, lmbda)
u = Function ('u', V, xx);
a = JacobianForm (problem, V, mu, lmbda, u);
L = ResidualForm (problem, V, mu, lmbda, B, T, u);
if (nargout == 1)
[y, xx] = assemble (L, xx, bc1, bc2);
elseif (nargout == 2)
[jac, y, xx] = assemble_system (a, L, xx, bc1, bc2);
endif
endfunction
fs = @(xx) f (problem, xx, V, bcl, bcr, B, T, mu, lmbda);
[x, fval, info] = fsolve (fs, u0, optimset ("jacobian", "on"));
func = Function ('u', V, x);
# Save solution in VTK format
save (func, 'displacement');
# Plot solution
plot (func);
|
| Code: Define HyperElasticity problem with fenics c++ |
#include <dolfin.h>
#include "HyperElasticity.h"
using namespace dolfin;
// Sub domain for clamp at left end
class Left : public SubDomain
{
bool inside(const Array<double>& x, bool on_boundary) const
{
return (std::abs(x[0]) < DOLFIN_EPS) && on_boundary;
}
};
// Sub domain for rotation at right end
class Right : public SubDomain
{
bool inside(const Array<double>& x, bool on_boundary) const
{
return (std::abs(x[0] - 1.0) < DOLFIN_EPS) && on_boundary;
}
};
// Dirichlet boundary condition for clamp at left end
class Clamp : public Expression
{
public:
Clamp() : Expression(3) {}
void eval(Array<double>& values, const Array<double>& x) const
{
values[0] = 0.0;
values[1] = 0.0;
values[2] = 0.0;
}
};
// Dirichlet boundary condition for rotation at right end
class Rotation : public Expression
{
public:
Rotation() : Expression(3) {}
void eval(Array<double>& values, const Array<double>& x) const
{
const double scale = 0.5;
// Center of rotation
const double y0 = 0.5;
const double z0 = 0.5;
// Large angle of rotation (60 degrees)
double theta = 1.04719755;
// New coordinates
double y = y0 + (x[1]-y0)*cos(theta) - (x[2]-z0)*sin(theta);
double z = z0 + (x[1]-y0)*sin(theta) + (x[2]-z0)*cos(theta);
// Rotate at right end
values[0] = 0.0;
values[1] = scale*(y - x[1]);
values[2] = scale*(z - x[2]);
}
};
int main()
{
// Create mesh and define function space
UnitCubeMesh mesh (16, 16, 16);
HyperElasticity::FunctionSpace V(mesh);
// Define Dirichlet boundaries
Left left;
Right right;
// Define Dirichlet boundary functions
Clamp c;
Rotation r;
// Create Dirichlet boundary conditions
DirichletBC bcl(V, c, left);
DirichletBC bcr(V, r, right);
std::vector<const BoundaryCondition*> bcs;
bcs.push_back(&bcl); bcs.push_back(&bcr);
// Define source and boundary traction functions
Constant B(0.0, -0.5, 0.0);
Constant T(0.1, 0.0, 0.0);
// Define solution function
Function u(V);
// Set material parameters
const double E = 10.0;
const double nu = 0.3;
Constant mu(E/(2*(1 + nu)));
Constant lambda(E*nu/((1 + nu)*(1 - 2*nu)));
// Create (linear) form defining (nonlinear) variational problem
HyperElasticity::ResidualForm F(V);
F.mu = mu; F.lmbda = lambda; F.B = B; F.T = T; F.u = u;
// Create jacobian dF = F' (for use in nonlinear solver).
HyperElasticity::JacobianForm J(V, V);
J.mu = mu; J.lmbda = lambda; J.u = u;
// Solve nonlinear variational problem F(u; v) = 0
solve(F == 0, u, bcs, J);
// Save solution in VTK format
File file("displacement.pvd");
file << u;
// Plot solution
plot(u);
interactive();
return 0;
}
© Copyright 2011, The FEniCS Project
|
[edit]
The incompressible Navier-Stokes equations are solved using the Chorin-Temam projection algorithm. [7]. A complete description of the specific problem is avilable on the Fenics website.
| Code: Define HyperElasticity problem with fem-fenics |
pkg load fem-fenics msh
import_ufl_Problem ("TentativeVelocity");
import_ufl_Problem ("VelocityUpdate");
import_ufl_Problem ("PressureUpdate");
# We can either load the mesh from the file as in Dolfin but
# we can also use the msh pkg to generate the L-shape domain
name = [tmpnam ".geo"];
fid = fopen (name, "w");
fputs (fid,"Point (1) = {0, 0, 0, 0.1};\n");
fputs (fid,"Point (2) = {1, 0, 0, 0.1};\n");
fputs (fid,"Point (3) = {1, 0.5, 0, 0.1};\n");
fputs (fid,"Point (4) = {0.5, 0.5, 0, 0.1};\n");
fputs (fid,"Point (5) = {0.5, 1, 0, 0.1};\n");
fputs (fid,"Point (6) = {0, 1, 0,0.1};\n");
fputs (fid,"Line (1) = {5, 6};\n");
fputs (fid,"Line (2) = {2, 3};\n");
fputs (fid,"Line(3) = {6,1,2};\n");
fputs (fid,"Line(4) = {5,4,3};\n");
fputs (fid,"Line Loop(7) = {3,2,-4,1};\n");
fputs (fid,"Plane Surface(8) = {7};\n");
fclose (fid);
msho = msh2m_gmsh (canonicalize_file_name (name)(1:end-4),...
"scale", 1,"clscale", .2);
unlink (canonicalize_file_name (name));
mesh = Mesh (msho);
# Define function spaces (P2-P1). From ufl file
# V = VectorElement("CG", triangle, 2)
# Q = FiniteElement("CG", triangle, 1)
V = FunctionSpace ('VelocityUpdate', mesh);
Q = FunctionSpace ('PressureUpdate', mesh);
# Define trial and test functions. From ufl file
# u = TrialFunction(V)
# p = TrialFunction(Q)
# v = TestFunction(V)
# q = TestFunction(Q)
# Set parameter values. From ufl file
# nu = 0.01
dt = 0.01;
T = 3.;
# Define boundary conditions
noslip = DirichletBC (V, @(x,y) [0; 0], [3, 4]);
outflow = DirichletBC (Q, @(x,y) 0, 2);
# Create functions
u0 = Expression ('u0', @(x,y) [0; 0]);
# Define coefficients
k = Constant ('k', dt);
f = Constant ('f', [0; 0]);
# Tentative velocity step. From ufl file
# eq = (1/k)*inner(u - u0, v)*dx + inner(grad(u0)*u0, v)*dx \
# + nu*inner(grad(u), grad(v))*dx - inner(f, v)*dx
a1 = BilinearForm ('TentativeVelocity', V, V, k);
# Pressure update. From ufl file
# a = inner(grad(p), grad(q))*dx
# L = -(1/k)*div(u1)*q*dx
a2 = BilinearForm ('PressureUpdate', Q, Q);
# Velocity update
# a = inner(u, v)*dx
# L = inner(u1, v)*dx - k*inner(grad(p1), v)*dx
a3 = BilinearForm ('VelocityUpdate', V, V);
# Assemble matrices
A1 = assemble (a1, noslip);
A3 = assemble (a3, noslip);
# Time-stepping
t = dt; i = 0;
while t < T
# Update pressure boundary condition
inflow = DirichletBC (Q, @(x,y) sin(3.0*t), 1);
# Compute tentative velocity step
"Computing tentative velocity"
L1 = LinearForm ('TentativeVelocity', V, k, u0, f);
b1 = assemble (L1, noslip);
utmp = A1 \ b1;
u1 = Function ('u1', V, utmp);
# Pressure correction
"Computing pressure correction"
L2 = LinearForm ('PressureUpdate', Q, u1, k);
[A2, b2] = assemble_system (a2, L2, inflow, outflow);
ptmp = A2 \ b2;
p1 = Function ('p1', Q, ptmp);
# Velocity correction
"Computing velocity correction"
L3 = LinearForm ('VelocityUpdate', V, k, u1, p1);
b3 = assemble (L3, noslip);
ut = A3 \ b3;
u1 = Function ('u0', V, ut);
# Plot solution
plot (p1);
plot (u1);
# Save to file
save (p1, sprintf ("p_%3.3d", ++i));
save (u1, sprintf ("u_%3.3d", i));
# Move to next time step
u0 = u1;
t += dt
end
|
| Code: Define NS problem with fenics python |
from dolfin import *
# Load mesh from file
mesh = Mesh("lshape.xml.gz")
# Define function spaces (P2-P1)
V = VectorFunctionSpace(mesh, "CG", 2)
Q = FunctionSpace(mesh, "CG", 1)
# Define trial and test functions
u = TrialFunction(V)
p = TrialFunction(Q)
v = TestFunction(V)
q = TestFunction(Q)
# Set parameter values
dt = 0.01
T = 3
nu = 0.01
# Define time-dependent pressure boundary condition
p_in = Expression("sin(3.0*t)", t=0.0)
# Define boundary conditions
noslip = DirichletBC(V, (0, 0),
"on_boundary && \
(x[0] < DOLFIN_EPS | x[1] < DOLFIN_EPS | \
(x[0] > 0.5 - DOLFIN_EPS && x[1] > 0.5 - DOLFIN_EPS))")
inflow = DirichletBC(Q, p_in, "x[1] > 1.0 - DOLFIN_EPS")
outflow = DirichletBC(Q, 0, "x[0] > 1.0 - DOLFIN_EPS")
bcu = [noslip]
bcp = [inflow, outflow]
# Create functions
u0 = Function(V)
u1 = Function(V)
p1 = Function(Q)
# Define coefficients
k = Constant(dt)
f = Constant((0, 0))
# Tentative velocity step
F1 = (1/k)*inner(u - u0, v)*dx + inner(grad(u0)*u0, v)*dx \
+ nu*inner(grad(u), grad(v))*dx - inner(f, v)*dx
a1 = lhs(F1)
L1 = rhs(F1)
# Pressure update
a2 = inner(grad(p), grad(q))*dx
L2 = -(1/k)*div(u1)*q*dx
# Velocity update
a3 = inner(u, v)*dx
L3 = inner(u1, v)*dx - k*inner(grad(p1), v)*dx
# Assemble matrices
A1 = assemble(a1)
A2 = assemble(a2)
A3 = assemble(a3)
# Use amg preconditioner if available
prec = "amg" if has_krylov_solver_preconditioner("amg")
else "default"
# Create files for storing solution
ufile = File("results/velocity.pvd")
pfile = File("results/pressure.pvd")
# Time-stepping
t = dt
while t < T + DOLFIN_EPS:
# Update pressure boundary condition
p_in.t = t
# Compute tentative velocity step
begin("Computing tentative velocity")
b1 = assemble(L1)
[bc.apply(A1, b1) for bc in bcu]
solve(A1, u1.vector(), b1, "gmres", "default")
end()
# Pressure correction
begin("Computing pressure correction")
b2 = assemble(L2)
[bc.apply(A2, b2) for bc in bcp]
solve(A2, p1.vector(), b2, "gmres", prec)
end()
# Velocity correction
begin("Computing velocity correction")
b3 = assemble(L3)
[bc.apply(A3, b3) for bc in bcu]
solve(A3, u1.vector(), b3, "gmres", "default")
end()
# Plot solution
plot(p1, title="Pressure", rescale=True)
plot(u1, title="Velocity", rescale=True)
# Save to file
ufile << u1
pfile << p1
# Move to next time step
u0.assign(u1)
t += dt
print "t =", t
# Hold plot
interactive()
© Copyright 2011, The FEniCS Project
|
Obstacles in the Domain[edit]
The above example is a weighted Poisson problem on the unit square. The diffusion coefficient assumes value 0.01 on the obstacle , whilst 1 outside on . You can find a detailed explanation on the FEniCS website. On the side, you can see the solution.
| Code: Define Poisson problem with obstacle with fem-fenics |
pkg load fem-fenics msh
# Create mesh
x = y = linspace (0, 1, 65);
[msh, facets] = Mesh (msh2m_structured_mesh (x, y, 0, 4:-1:1));
ufl start Subdomains
ufl fe = FiniteElement "(""CG"", triangle, 2)"
ufl u = TrialFunction (fe)
ufl v = TestFunction (fe)
ufl
ufl a0 = Coefficient (fe)
ufl a1 = Coefficient (fe)
ufl g_L = Coefficient (fe)
ufl g_R = Coefficient (fe)
ufl f = Coefficient (fe)
ufl
ufl a= "inner(a0*grad(u),grad(v))*dx(0) + inner(a1*grad(u),grad(v))*dx(1)"
ufl L = g_L*v*ds(1) + g_R*v*ds(3) + f*v*dx(0) + f*v*dx(1)
ufl end
V = FunctionSpace ("Subdomains", msh);
# Define problem coefficients
a0 = Constant ("a0", 1.0);
a1 = Constant ("a1", 0.01);
g_L = Expression ("g_L", @(x, y) - 10*exp(- (y - 0.5) ^ 2));
g_R = Constant ("g_R", 1.0);
f = Constant ("f", 1.0);
# Define subdomains
domains = MeshFunction ("dx", msh, 2, 0);
obstacle = SubDomain (@(x,y) (y >= 0.5) && (y <= 0.7) && ...
(x >= 0.2) && (x <= 1.0), false);
domains = mark (obstacle, domains, 1);
# Define boundary conditions
bc1 = DirichletBC (V, @(x, y) 5.0, facets, 2);
bc2 = DirichletBC (V, @(x, y) 0.0, facets, 4);
# Define variational form
a = BilinearForm ("Subdomains", V, V, a0, a1, domains);
L = LinearForm ("Subdomains", V, g_L, g_R, f, facets, domains);
# Solve problem
[A, b] = assemble_system (a, L, bc1, bc2);
sol = A \ b;
u = Function ("u", V, sol);
# Plot solution
[X, Y] = meshgrid (x, y);
U = u (X, Y);
surf (X, Y, U);
|
| Code: Define Poisson problem with obstacle with FEniCS python |
from dolfin import *
# Define mesh
mesh = UnitSquareMesh(64, 64)
# Create classes for defining parts of the boundaries
class Left(SubDomain):
def inside(self, x, on_boundary):
return near(x[0], 0.0)
class Right(SubDomain):
def inside(self, x, on_boundary):
return near(x[0], 1.0)
class Bottom(SubDomain):
def inside(self, x, on_boundary):
return near(x[1], 0.0)
class Top(SubDomain):
def inside(self, x, on_boundary):
return near(x[1], 1.0)
# Initialize sub-domain instances
left = Left()
top = Top()
right = Right()
bottom = Bottom()
# Initialize mesh function for boundary domains
boundaries = FacetFunction("size_t", mesh)
boundaries.set_all(0)
left.mark(boundaries, 1)
top.mark(boundaries, 2)
right.mark(boundaries, 3)
bottom.mark(boundaries, 4)
# Define function space and basis functions
V = FunctionSpace(mesh, "CG", 2)
u = TrialFunction(V)
v = TestFunction(V)
# Define input data
a0 = Constant(1.0)
a1 = Constant(0.01)
g_L = Expression("- 10*exp(- pow(x[1] - 0.5, 2))")
g_R = Constant("1.0")
f = Constant(1.0)
# Initialize mesh function for interior domains
class Obstacle(SubDomain):
def inside(self, x, on_boundary):
return (between(x[1], (0.5, 0.7)) and between(x[0], (0.2, 1.0)))
obstacle = Obstacle()
domains = CellFunction("size_t", mesh)
domains.set_all(0)
obstacle.mark(domains, 1)
# Define Dirichlet boundary conditions at top and bottom boundaries
bcs = [DirichletBC(V, 5.0, boundaries, 2),
DirichletBC(V, 0.0, boundaries, 4)]
# Define new measures associated with the interior domains and
# exterior boundaries
dx = Measure("dx")[domains]
ds = Measure("ds")[boundaries]
# Define variational form
F = (inner(a0*grad(u), grad(v))*dx(0) + inner(a1*grad(u), grad(v))*dx(1)
- g_L*v*ds(1) - g_R*v*ds(3)
- f*v*dx(0) - f*v*dx(1))
# Separate left and right hand sides of equation
a, L = lhs(F), rhs(F)
# Solve problem
u = Function(V)
solve(a == L, u, bcs)
# Plot solution
plot(u, title="u")
interactive()
© Copyright 2011, The FEniCS Project
|
Relevant Implementation Details[edit]
The relevant implementation details which the user should know are:
- All the objects are managed using boost::shared_ptr <>. It means that the same resource can be shared by more objects and useless copies should be avoided. For example, if we have two different functional spaces in the same problem, like with Navier-Stokes for the velocity and the pressure, the mesh is shared between them and no one has its own copy.
- The essential BC are imposed directly to the matrix with the command assemble(), which sets to zero all the off diagonal elements in the corresponding line, sets to 1 the diagonal element and sets to the exact value the rhs. This means that we could loose the symmetry of the matrix, if any. To avoid this problem and preserve the symmetry of the system it is available the assemble_system() command which builds at once the lhs and the rhs.
- The coefficient of the variational problem can be specified using either an Expression(), a Constant() or a Function(). They are different objects which behave in different ways: an Expression or a Constant object overloads the eval() method of the dolfin::Expression class and it is evaluated at run time using the octave function feval (). A Function instead doesn't need to be evaluated because it is assembled copying element-by-element the values contained in the input vector.
- Unfortunately the feature used in previous versions of the package to handle DirichletBC is not implemented yet in the FEniCS library for distributed execution. This means that prior to running code via MPI it should be adapted to use the newly introduced MeshFunction to mark border subsets, so that essential boundary conditions are correctly applied.
Known issues[edit]
- Fem-fenics needs both in the installation phase and in normal usage some includes that are not in standard system include directories, namely those related to MPI and the Eigen template library. If you experience an installation failure or errors when importing your UFL files, then you should properly set your CPPFLAGS environment variable before launching Octave, as per [8]. This can be done in sh compatible shells with the command below:
export CPPFLAGS="-I/usr/include/eigen3 $(mpicxx -showme:compile)"
Notice that /usr/include/eigen3 has to be changed accordingly to the path in which Eigen are to be found on your system.
It should readily work in Ubuntu 13.10 and 14.04.
- There is a known bug with Openmpi, discussed on the maintainers list [9], that needs the preloading of a MPI shared library with the following command:
export LD_PRELOAD=/usr/lib/openmpi/lib/libmpi.so
Again, notice that /usr/lib/openmpi/lib/libmpi.so has to be changed to fit to your system.
Additional functionality / TODOS[edit]
Obviously, Fem-fenics is not (yet) able to reproduce all the functionality available in Fenics. If there is any important features missing, please add it to the list below. (Or, better, you can directly submit your extension to the mercurial repository [10]).
- Normal: add the possibility to use a reserved keyword (normal ?) to be used with the DirichletBC.
bc = DirichletBC (V, @(x, y, normal) [sin(x)*normal; 0], [3, 4]);
@function/feval: the function should accept as input also an array of values.Show how it can be used in an example with odepkg.














![{\displaystyle \Omega _{1}=[0.5,0.7]\times [0.2,1.0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/850492c5bba42b3ef3f20e7863ffbf75234ac675)
