Cookbook
An Octave cookbook. Each entry should go in a separate section and have the following subsection: problem, solution, discussion and maybe a see also.
Structures
Retrieve a field value from all entries in a struct array
Problem
You have a struct array with multiple fields, and you want to acess the value from a specific field from all elements. For example, you want to return the age from all patients in the following case:
samples = struct ("patient", {"Bob", "Kevin", "Bob" , "Andrew"},
"age", [ 45 , 52 , 45 , 23 ],
"protein", {"H2B", "CDK2" , "CDK2", "Tip60" },
"tube" , [ 3 , 5 , 2 , 18 ]
);
Solution
Indexing the struct returns a comma separated list so use them to create a matrix.
[samples(:).age]
This however does not keep the original structure of the data, instead returning all values in a single column. To fix this, use reshape().
reshape ([samples(:).age], size (samples))
Discussion
Returning all values in a comma separated lists allows you to make anything out of them. If numbers are expected, create a matrix by enclosing them in square brackets. But if strings are to be expected, a cell array can also be easily generated with curly brackets
{samples(:).name}
You are also not limited to return all elements, you may use logical indexing from other fields to get values from the others:
[samples([samples(:).age] > 34).tube] ## return tube numbers from all samples from patients older than 34
[samples(strcmp({samples(:).protein}, "CDK2").tube] ## return all tube numbers for protein CDK2
Input/output
Mathematics
Find if a number is even/odd
Problem
You have a number, or an array or matrix of them, and want to know if any of them is an odd or even number, i.e., their parity.
Solution
Check the remainder of a division by two. If the remainder is zero, the number is odd.
mod (value, 2) ## 1 if odd, zero if even
Since mod() acceps a matrix, the following can be done:
any (mod (values, 2)) ## true if at least one number in values is even all (mod (values, 2)) ## true if all numbers in values are odd any (!logical (mod (values, 2))) ## true if at least one number in values is even all (!logical (mod (values, 2))) ## true if all numbers in values are even
Discussion
Since we are checking for the remainder of a division, the first choice would be to use rem(). However, in the case of negative numbers mod() will still return a positive number making it easier for comparisons. Another alternative is to use bitand (X, 1) or bitget (X, 1) but those are a bit slower.
Note that this solution applies to integers only. Non-integers such as 1/2 or 4.201 are neither even nor odd. If the source of the numbers are unknown, such as user input, some sort of checking should be applied for NaN, Inf, or non-integer values.
See also
Find if a number is an integer.
Parametrized Functions
Problem
One sometimes needs to define a family of functions depending on a set of parameters, e.g.,
where
denote a the variables on which the function operates and
are the parameters used to chose one specific element of the family of functions.
For example, let's say we need to compute the time evolution of the elongation of a spring for different values of the spring constant
Solution
We could solve the problem with the following code
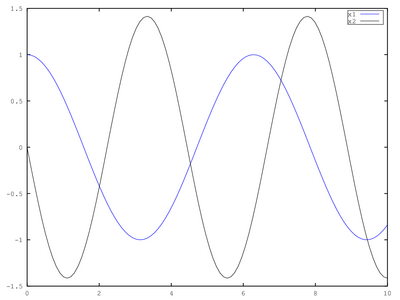
| Code: Solve spring equation for different values of the spring constant |
t = linspace (0, 10, 100);
function sprime = spring (s, t, k)
x = s(1);
v = s(2);
sprime(1) = v;
sprime(2) = -k * x;
endfunction
k = 1;
x1 = lsode (@(x, t) spring (x, t, k), [1;0], t)(:, 1);
k = 2;
x2 = lsode (@(x, t) spring (x, t, k), [1;0], t)(:, 2);
plot (t, x1, t, x2)
legend ('x1', 'x2')
|
Discussion
In the above example, the function "sprime" represents a family of functions of the variables
parametrized by the parameter
.
@(x, t) sprime (x, t, k)
is a function of only where the parameter is 'frozen' to the value it has at the moment in the current scope.