Bim package
Package for solving Diffusion Advection Reaction (DAR) Partial Differential Equations based on the Finite Volume Scharfetter-Gummel (FVSG) method a.k.a Box Integration Method (BIM).
Tutorials
2D Diffusion Advection Reaction example
This is a short example on how to use bim to solve a 2D Diffusion Advection Reaction problem. The coplete code for this example can is on Agora at this link.
We want to solve the equation
with mixed Dirichlet / Neumann boundary conditions
Create the mesh and precompute the mesh properties
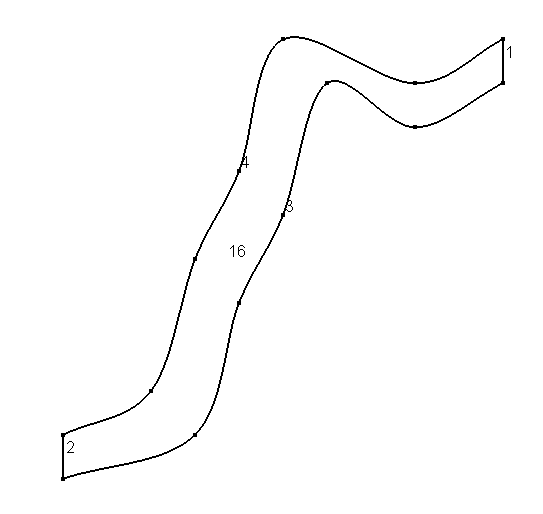
To define the geometry of the domain we can use gmsh.
the following gmsh input
Point (1) = {0, 0, 0, 0.1};
Point (2) = {1, 1, 0, 0.1};
Point (3) = {1, 0.9, 0, 0.1};
Point (4) = {0, 0.1, 0, 0.1};
Point (5) = {0.3,0.1,-0,0.1};
Point (6) = {0.4,0.4,-0,0.1};
Point (7) = {0.5,0.6,0,0.1};
Point (8) = {0.6,0.9,0,0.1};
Point (9) = {0.8,0.8,0,0.1};
Point (10) = {0.2,0.2,-0,0.1};
Point (11) = {0.3,0.5,0,0.1};
Point (12) = {0.4,0.7,0,0.1};
Point (13) = {0.5,1,0,0.1};
Point (14) = {0.8,0.9,0,0.1};
Line (1) = {3, 2};
Line (2) = {4, 1};
CatmullRom(3) = {1,5,6,7,8,9,3};
CatmullRom(4) = {4,10,11,12,13,14,2};
Line Loop(15) = {3,1,-4,2};
Plane Surface(16) = {15};
will produce the geometry below
we need to load the mesh into Octave and precompute mesh properties check out the tutorial for the msh package for info on the mesh structure
| Code: Meshing the 2D problem |
[mesh] = msh2m_gmsh ("fiume","scale",1,"clscale",.1);
[mesh] = bim2c_mesh_properties (mesh);
|
to see the mesh you can use functions from the fpl package
| Code: Visualizing the mesh for the 2D problem |
pdemesh (mesh.p, mesh.e, mesh.t)
view (2)
|
Set the coefficients for the problem:
Get the node coordinates from the mesh structure
| Code: Get mesh coordinates in the 2D problem |
xu = mesh.p(1,:).';
yu = mesh.p(2,:).';
|
Get the number of elements and nodes in the mesh
| Code: Get number of elements in the 2D problem |
nelems = columns (mesh.t);
nnodes = columns (mesh.p);
|
| Code: Set value of coefficients for the 2D problem |
epsilon = .1;
phi = xu + yu;
|
Construct the discretized operators
| Code: Discretized operators for the 2D problem |
AdvDiff = bim2a_advection_diffusion (mesh, epsilon, 1, 1, phi);
Mass = bim2a_reaction (mesh, 1, 1);
b = bim2a_rhs (mesh,f,g);
A = AdvDiff + Mass;
|
To Apply Boundary Conditions, partition LHS and RHS
The tags of the sides are assigned by gmsh we let be composed by sides 1 and 2 and be the rest of the boundary
| Code: Boundary conditions for the 2D problem |
GammaD = bim2c_unknowns_on_side (mesh, [1 2]); ## DIRICHLET NODES LIST
GammaN = bim2c_unknowns_on_side (mesh, [3 4]); ## NEUMANN NODES LIST
GammaN = setdiff (GammaN, GammaD);
jn = zeros (length (GammaN),1); ## PRESCRIBED NEUMANN FLUXES
ud = 3*xu; ## DIRICHLET DATUM
Omega = setdiff (1:nnodes, union (GammaD, GammaN)); ## INTERIOR NODES LIST
Add = A(GammaD, GammaD);
Adn = A(GammaD, GammaN); ## shoud be all zeros hopefully!!
Adi = A(GammaD, Omega);
And = A(GammaN, GammaD); ## shoud be all zeros hopefully!!
Ann = A(GammaN, GammaN);
Ani = A(GammaN, Omega);
Aid = A(Omega, GammaD);
Ain = A(Omega, GammaN);
Aii = A(Omega, Omega);
bd = b(GammaD);
bn = b(GammaN);
bi = b(Omega);
|
Solve for the tracer density
| Code: Compute solution of the 2D problem |
temp = [Ann Ani ; Ain Aii ] \ [ jn+bn-And*ud(GammaD) ; bi-Aid*ud(GammaD)];
u = ud;
u(GammaN) = temp(1:numel (GammaN));
u(Omega) = temp(length(GammaN)+1:end);
|
Compute the fluxes through Dirichlet sides
| Code: Boundary fluxes in the 2D problem |
jd = [Add Adi Adn] * u([GammaD; Omega; GammaN]) - bd;
|
Compute the gradient of the solution
| Code: Gradient of solution in the 2D problem |
[gx, gy] = bim2c_pde_gradient (mesh, u);
|
Compute the internal Advection-Diffusion flux
| Code: Total flux for the 2D problem |
[jxglob, jyglob] = bim2c_global_flux (mesh, u, epsilon*ones(nelems, 1), ones(nnodes, 1), ones(nnodes, 1), phi);
|
Export data to VTK format
The resut can be exported to vtk format to visualize with [[1]] or [[2]]
| Code: Export the solution of the 2D problem to vtk |
fpl_vtk_write_field ("vtkdata", mesh, {u, "Solution"}, {[gx; gy]', "Gradient"}, 1);
|
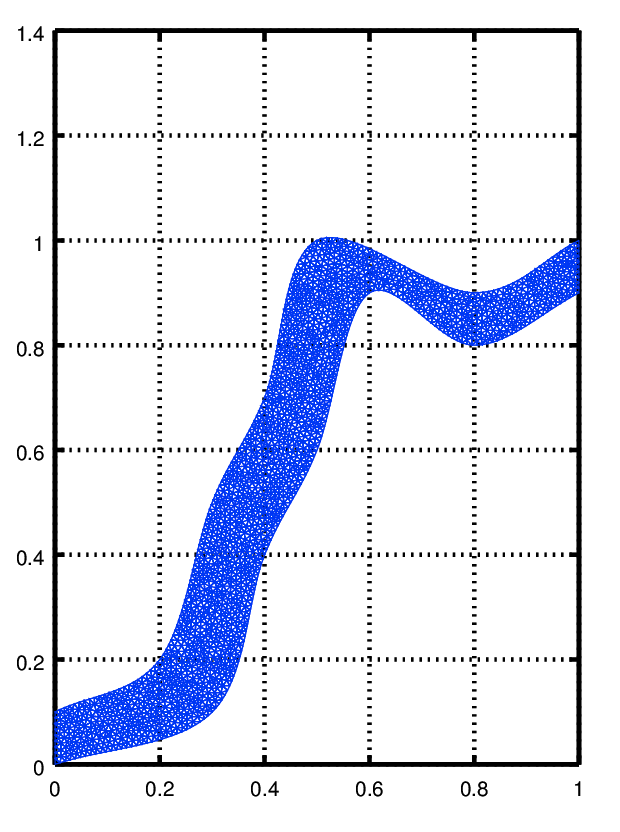
you can also plot your data directly in Octave using pdesurf
| Code: Rubbersheet visualization of the solution of the 2D problem |
pdesurf (mesh.p, mesh.t, u)
|
it will look like this
3D Time dependent problem
Here is an example of a 3D time-dependent Advection-Diffusion equation that uses lsode for time-stepping.
The equation being solved is
The initial condition is
| Code: Define the 3D problem |
pkg load bim
x = linspace (0, 1, 40);
y = z = linspace (0, 1, 20);
msh = bim3c_mesh_properties (msh3m_structured_mesh (x, y, z, 1, 1:6));
nn = columns (msh.p);
ne = columns (msh.t);
x = msh.p(1, :).';
y = msh.p(2, :).';
z = msh.p(3, :).';
x0 = .2; sx = .1;
y0 = .2; sy = .1;
z0 = .8; sz = .1;
u = exp (- ((x-x0)/(2*sx)) .^2 - ((y-y0)/(2*sy)) .^2 - ((z-z0)/(2*sz)) .^2);
A = bim3a_advection_diffusion (msh, .01*ones(ne, 1), 100*(x+y-z));
M = bim3a_reaction (msh, 1, 1);
function du = f (u, t, A, M)
du = - M \ (A * u);
endfunction
time = linspace (0, 1, 30);
lsode_options ("integration method", "adams");
U = lsode (@(u, t) f(u, t, A, M), u, time);
for ii = 1:1:numel (time)
name = sprintf ("u_%3.3d", ii);
delete ([name ".vtu"]);
fpl_vtk_write_field (name, msh, {U(ii,:)', 'u'}, {}, 1);
endfor
|
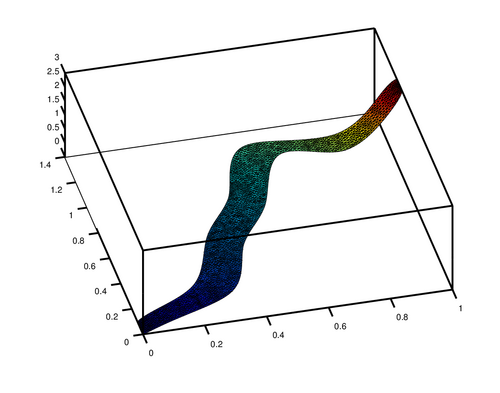
This is a video showing the .3 isosurface of the solution.





![{\displaystyle {\frac {\partial u}{\partial t}}-\mathrm {div} \left(.01\nabla u-u\nabla \varphi \right)=0\qquad {\mbox{ in }}\Omega \times [0,T]=[0,1]^{3}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3733151631f4fa649cf6dc34c0433c240f6a9c08)


