Cookbook

An Octave cookbook. Each entry should go in a separate section and have the following subsection: problem, solution, discussion and maybe a see also.

Structures

Retrieve a field value from all entries in a struct array

Problem

You have a struct array with multiple fields, and you want to acess the value from a specific field from all elements. For example, you want to return the age from all patients in the following case:

 samples = struct ("patient", {"Bob", "Kevin", "Bob" , "Andrew"},
                   "age",     [ 45  ,  52    ,  45   ,  23     ],
                   "protein", {"H2B", "CDK2" , "CDK2", "Tip60" },
                   "tube"   , [ 3   ,  5     ,  2    ,  18     ]
                   );

Solution

Indexing the struct returns a comma separated list so use them to create a matrix.

 [samples(:).age]

This however does not keep the original structure of the data, instead returning all values in a single column. To fix this, use reshape().

 reshape ([samples(:).age], size (samples))

Discussion

Returning all values in a comma separated lists allows you to make anything out of them. If numbers are expected, create a matrix by enclosing them in square brackets. But if strings are to be expected, a cell array can also be easily generated with curly brackets

 {samples(:).name}

You are also not limited to return all elements, you may use logical indexing from other fields to get values from the others:

 [samples([samples(:).age] > 34).tube]                 ## return tube numbers from all samples from patients older than 34
 [samples(strcmp({samples(:).protein}, "CDK2").tube]   ## return all tube numbers for protein CDK2

Mathematics

Find if a number is even/odd

Problem

You have a number, or an array or matrix of them, and want to know if any of them is an odd or even number, i.e., their parity.

Solution

Check the remainder of a division by two. If the remainder is zero, the number is odd.

 mod (value, 2) ## 1 if odd, zero if even

Since mod() acceps a matrix, the following can be done:

 any  (mod (values, 2)) ## true if at least one number in values is even
 all  (mod (values, 2)) ## true if all numbers in values are odd
 
 any (!logical (mod (values, 2))) ## true if at least one number in values is even
 all (!logical (mod (values, 2))) ## true if all numbers in values are even

Discussion

Since we are checking for the remainder of a division, the first choice would be to use rem(). However, in the case of negative numbers mod() will still return a positive number making it easier for comparisons. Another alternative is to use bitand (X, 1) or bitget (X, 1) but those are a bit slower.

Note that this solution applies to integers only. Non-integers such as 1/2 or 4.201 are neither even nor odd. If the source of the numbers are unknown, such as user input, some sort of checking should be applied for NaN, Inf, or non-integer values.

See also

Find if a number is an integer.

Parametrized Functions

Problem

One sometimes needs to define a family of functions depending on a set of parameters, e.g.,

$f(x,y,z;a,b,c)$

where

$x,y,z$ denote a the variables on which the function operates and

$a,b,c$

are the parameters used to chose one specific element of the family of functions.

For example, let's say we need to compute the time evolution of the elongation of a spring for different values of the spring constant

$k$

Solution

We could solve the problem with the following code

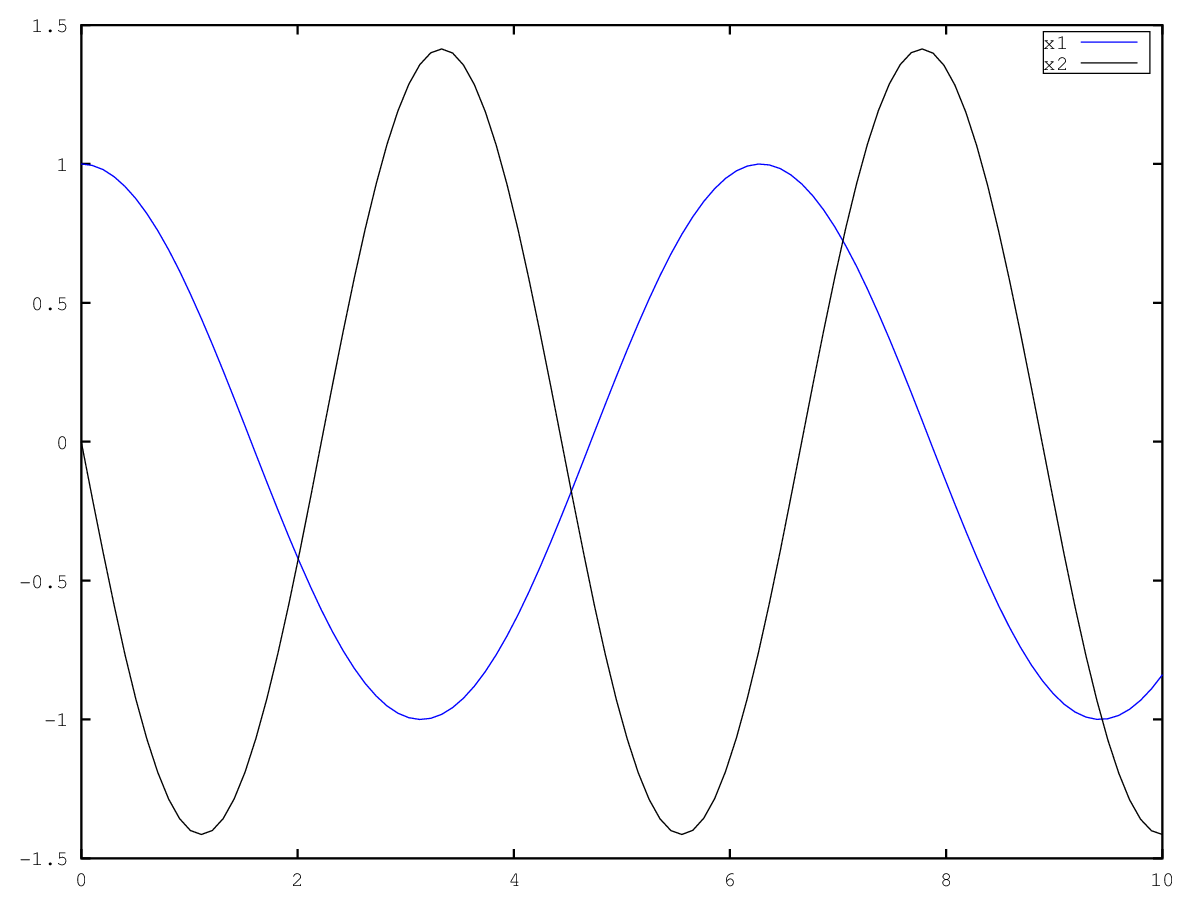
Code: Solve spring equation for different values of the spring constant

t = linspace (0, 10, 100); function sprime = spring (s, t, k) x = s(1); v = s(2); sprime(1) = v; sprime(2) = -k * x; endfunction k = 1; x1 = lsode (@(x, t) spring (x, t, k), [1;0], t)(:, 1); k = 2; x2 = lsode (@(x, t) spring (x, t, k), [1;0], t)(:, 2); plot (t, x1, t, x2) legend ('x1', 'x2')

Discussion

In the above example, the function "sprime" represents a family of functions of the variables

$x,t$

parametrized by the parameter

$k$.

The anonympus function

  @(x, t) sprime (x, t, k)

is a function of only $x,t$ where the parameter $k$ is 'frozen' to the value it has at the moment in the current scope.