TISEAN package

From Octave
Revision as of 16:05, 11 August 2015 by Josiah425 (talk | contribs) (→‎Porting TISEAN: merged Portinf into main)
Jump to navigation Jump to search

Porting TISEAN

This section will focus on demonstrating the capabilities of the TISEAN package.

Process

This section describes the process employed during porting TISEAN package into an Octave Package. This project was started as part of the Google Summer of Code 2015.

To aid in understanding the task there are some charts.

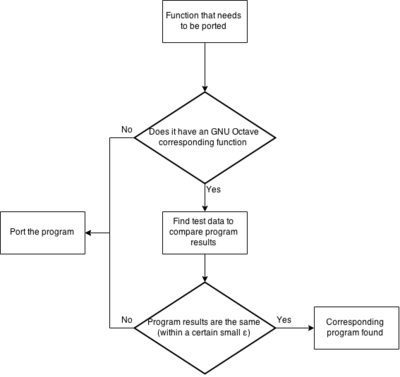
The first chart depicts what to do with each function in the function table. I mainly focuses on those functions that might already implemented in Octave.

Work flow TISEAN.png

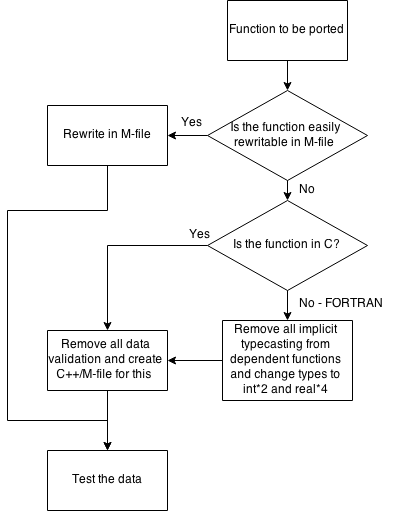
The chart below depicts how to decide which type of port should be utilized.

Porting Programs TISEAN.png

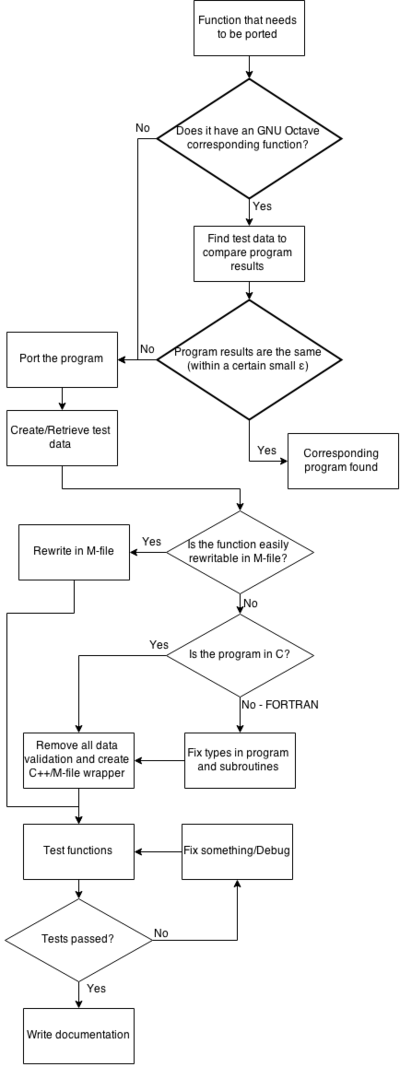
Both of those charts can be combined into a large one that shows all of the work together.

Flow Together TISEAN.png

Table of functions and progress

In reference to the TISEAN library alphabetical order of programs which is located here.

The choice whether a program exist in Octave is based only on comparing package/octave documentation with the TISEAN documentation. As of now I have not compared any code, nor checked if any sample data gives the same results from both functions (the octave ones and the TISEAN ones).

The legend to understand the table is as follows:

Green means the function is ported, tested or is not needed
Red means the function was thought to have been similar but isn't
Yellow means that the correlation between the TISEAN and Octave function needs to be verified
No color means that nothing about this function has been determined
Program Name Program Description Corresponding Octave Function Lanuguage of Origin How to port Status
arima-model Fit and possibly iterate an ARIMA model generalizes TSA arma functions C wrapped in C++/mfile/octfile code
ar-model Fit and possibly iterate an Autoregessive model 'aar' in TSA; see also: aarmam, adim, amarma, mvaar from TSA C wrapped in C++/mfile/octfile code
ar-run Iterate an Autoregessive model Same as above FORTRAN wrapped in C++/mfile/octfile code
av-d2 Simply smooth output of d2 Can be implemented with filter in core C
boxcount Renyi Entopies of Qth order None in GNU Octave (maybe in info-theory but it is not worth the pain) C wrapped in C++/mfile/octfile code
c1 Fixed mass estimation of D1 None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code
c2d Get local slopes from correlation integral None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code
c2g Gaussian kernel of C2 None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code
c2t Takens estimator of D2 None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code
choose Choose rows and/or columns from a data file Does not need to be ported FORTRAN ----- Not Needed
compare Compares two data sets Does not need to be ported FORTRAN ------ Not Needed
corr, autocorr Autocorrelation function xcorr in signal corr -C, autocorr (faster according to documentation) - FORTRAN ------- Different usage, same result
d2 Correlation dimension d2 None in GNU Octave C wrapped in C++/mfile/octfile code
delay Creates delay embedding None in GNU Octave (easy to implement in Octave but not worth the effort) C wrapped in C++/mfile/octfile code Ported&Tested
endtoend Determine end-to-end mismatch None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code Ported&Tested
events Interval/event conversion None in GNU Octave FORTRAN To be reimplemented as m-file
extrema Determine the extrema of a time series findpeaks in signal is *not* the same C
false_nearest The false nearest neighbor algorithm None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
ghkss Nonlinear noise reduction None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
henon Create a Hénon time series None in GNU Octave FORTRAN To be reimplemented as m-file Ported&Checked
histogram Creates histograms hist in core C Different usage, same result
ikeda Create an Ikeda time series None in GNU Octave FORTRAN To be reimplemented as mfile Ported&Tested
intervals Event/intervcal conversion Might exist under different name FORTRAN To be reimplemented as mfile
lazy Simple nonlinear noise reduction None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code Ported&Tested
lfo-ar Locally first order model vs. global AR model (old ll-ar) None in GNU Octave C wrapped in C++/mfile/octfile code
lfo-run Iterate a locally first order model (old nstep) None in GNU Octave C wrapped in C++/mfile/octfile code
lfo-test Test a locally first order model (old onestep) None in GNU Octave C wrapped in C++/mfile/octfile code
lorenz Create a Lorenz time series Can be implemented in GNU Octave using lsode or odepkg FORTRAN mfile
low121 Time domain low pass filter There are lowpass filters in Octave: buttap, cheb1ap, cheb2ap, ellipap, sftrans, but I don't think they perform this task C Reimplement as mfile
lyap_k Maximal Lyapunov exponent with the Kantz algorithm None in GNU Octave C wrapped in C++/mfile/octfile code
lyap_r Maximal Lyapunov exponent with the Rosenstein algorithm None in GNU Octave C wrapped in C++/mfile/octfile code
lyap_spec Full spectrum of Lyapunov exponents None in GNU Octave C wrapped in C++/mfile/octfile code
lzo-gm Locally zeroth order model vs. global mean None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
lzo-run Iterate a locally zeroth order model None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
lzo-test Test a locally zeroth order model (old zeroth) None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
makenoise Produce noise Rand exists Should be implemented as mfile using Octave rand functions wrapped in C++/mfile/octfile code
mem_spec Power spectrum using the maximum entropy principle None in GNU Octave C wrapped in C++/mfile/octfile code
mutual Estimate the mutual information None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
notch Notch filter pei_tseng_notch, needs to be verified FORTRAN wrapped in C++/mfile/octfile code
nstat_z Nonstationarity testing via cross-prediction None in GNU Octave C wrapped in C++/mfile/octfile code
pca, pc Principle component analysis 'pcacov' if likely the equivalent; pricomp in statistics pca - C, pc - FORTRAN wrapped in C++/mfile/octfile code Ported&Tested
poincare Create Poincaré sections None in GNU Octave C wrapped in C++/mfile/octfile code Ported&Tested
polyback Fit a polynomial model (backward elimination) polyfit, detrend, wpolyfit are not similar C wrapped in C++ Porting needed
polynom Fit a polynomial model same as above C Ported&Tested
polynomp Fit a polynomial model (reads terms to fit from file) same as above C
polypar Creates parameter file for polynomp same as above C
predict Forecast discriminating statistics for surrogates None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code Same as lzo_test; Not Needed
randomize General constraint randomization (surrogates) There are random function, but I don't think this one exists FORTRAN wrapped in C++/mfile/octfile code
randomize_spikeauto_exp_random Surrogate data preserving event time autocorrelations Same as above FORTRAN wrapped in C++/mfile/octfile code
randomize_spikespec_exp_event Surrogate data preserving event time power spectrum Same as above FORTRAN wrapped in C++/mfile/octfile code
rbf Radial basis functions fit None in GNU Octave C wrapped in C++/mfile/octfile code
recurr Creates a recurrence plot None in GNU Octave C wrapped in C++/mfile/octfile code
resample Resamples data interp1 is similar but cannot specify the polynomial order except for some given C wrapped in C++/mfile/octfile code
rescale Rescale data set This is just multiplication by scalars C wrapped in C++/mfile/octfile code Not Needed
rms Rescale data set and get mean, variance and data interval This should be in Octave, cannot find... FORTRNAN wrapped in C++/mfile/octfile code Not Needed
sav_gol Savitzky-Golay filter sgolayfilt in signal C
spectrum Power spectrum using FFT abs (fft (;)) FORTRAN Rewrite as m-file Ported&Tested
spikeauto Autocorrelation function of event times similar to above FORTRAN
spikespec Power spectrum of event times ar_psd, cpsd is the closest but I do not think they are the same FORTRAN
stp Creates a space-time separation plot None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code
surrogates Creates surrogate data None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code Ported&Tested
timerev Time reversal discrimating statistics for surrogates None in GNU Octave FORTRAN To be reimplemented as mfile Ported&Tested
upo Finds unstable periodic orbits and estimates their stability None in GNU Octave FORTRAN wrapped in C++/mfile/octfile code Ported&Tested
upoembed Takes the output of upo and create data files out of it None in GNU Octave FORTAN wrapped in C++/mfile/octfile code Ported&Tested
wiener1, wiener2 Wiener filter Wiener process exists, might be similar FORTRAN wrapped in C++/mfile/octfile code
xc2 Cross-correlation integral xcorr2 - Needs to be verified that works the same way FORTRAN wrapped in C++/mfile/octfile code
xcor Cross-correlations xcorr - Needs to be verified that works same way C wrapped in C++/mfile/octfile code
xrecur Cross-recurrence Plot xcorr, or xcorr2 or another function might cover this C wrapped in C++/mfile/octfile code
xzero Locally zeroth order cross-prediction None in GNU Octave C wrapped in C++/mfile/octfile code

Tutorials

These tutorials are based on examples, tutorials and the articles located on the TISEAN website:
http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/.
This tutorial will utilize the following dataset:

Please download it as the tutorial will reference it.

False Nearest Neighbors

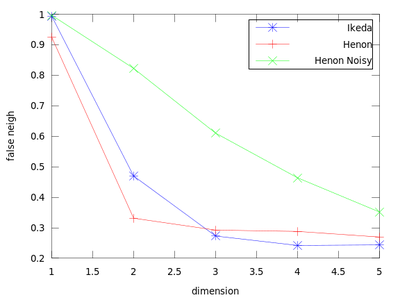
This function uses a method to determine the minimum sufficient embedding dimension. It is based on the False Nearest Neighbors section of the TISEAN documentation. As a demonstration we will create a plot that contains an Ikeda Map, a Henon Map and a Henon Map corrupted by 10% of Gaussian noise.

Code: Analyzing false nearest neighbors 
# Create maps
ikd       = ikeda (10000);
hen       = henon (10000);
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));
# Create and plot false nearest neighbors
[dim_ikd, frac_ikd] = false_nearest (ikd(:,1));
[dim_hen, frac_hen] = false_nearest (hen(:,1));
[dim_hen_noisy, frac_hen_noisy] = false_nearest (hen_noisy(:,1));
plot (dim_ikd, frac_ikd, '-b*;Ikeda;',...
      dim_hen, frac_hen, '-r+;Henon;',...
      dim_hen_noisy, frac_hen_noisy, '-gx;Henon Noisy;');

The dim_* variables hold the dimension (so here 1:5), and frac_* contain the fraction of false nearest neighbors. From this chart we can obtain the sufficient embedding dimension for each system. For a Henon Map m = 2 is sufficient, but for an Ikeda map it is better to use m = 3.

Tisean false neigh.png

Finding Unstable Periodic Orbits

Here I will demonstrate how to find unstable periodic orbits. This section is based on the TISEAN documentation chapter Finding unstable periodic orbits. We will start by finding these orbits using function upo.

Code: Finding unstable periodic orbits 
# Create maps
hen             = henon (1000);
hen             = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));
# Find orbits
[lengths, data] = upo(hen(:,1), 2, 'p',6,'v',0.1, 'n', 100);

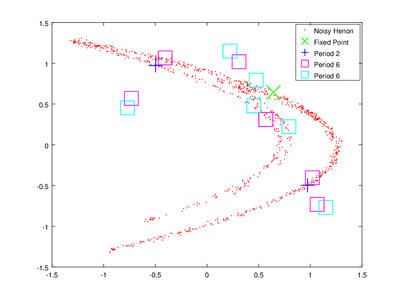
The vector lengths contains the size of each of the found orbits and data contains their coordinates. To obtain delay coordinates and plot these orbits onto the original data we will use upoembed.

Code: Plotting unstable periodic orbits 
# Create delay coordinates for the orbits and data
up        = upoembed (lengths, data, 1);
delay_hen = delay (hen(:,1));
# Plot all of the data
plot (delay_hen(:,1), delay_hen(:,2), 'r.;Noisy Henon;','markersize',2,...
      up{4}(:,1), up{4}(:,2),'gx;Fixed Point;','markersize',20,'linewidth',1, ...
      up{3}(:,1), up{3}(:,2),'b+;Period 2;','markersize',20,'linewidth',1, ...
      up{2}(:,1), up{2}(:,2),'ms;Period 6;','markersize',20,'linewidth',1, ...
      up{1}(:,1), up{1}(:,2),'cs;Period 6;','markersize',20,'linewidth',1);
Upo.png

The plotting options are passed to make the orbits more visible.

Nonlinear Prediction

In this section we will demonstrate some functions from the 'Nonlinear Prediction' chapter of the TISEAN documentation (located here). For now this section will only demonstrate functions that are connected to the Simple Nonlinear Prediction section.
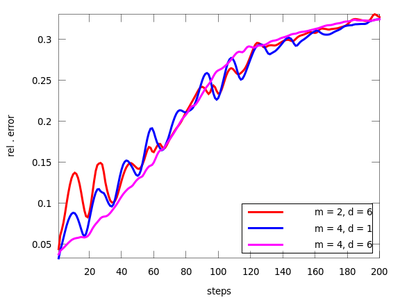
There are three functions in this section: lzo_test, lzo_gm and lzo_run. The first is used to estimate the forecast error for a set of chosen parameters, the second gives some global information about the fit and the third produces predicted points. Let us start with the first one (before starting this example remember to download 'amplitude.dat' from above and start Octave in the directory that contains it). The pairs of parameters (m,d) where chosen after the TISEAN documentation.

Code: Analyzing forecast errors for various parameters 
# Load data
load amplitude.dat
# Create different forecast error results
steps = 200;
res1  = lzo_test (amplitude(1:end-200), 'm', 2, 'd', 6, 's', steps);
res2  = lzo_test (amplitude(1:end-200), 'm', 3, 'd', 6, 's', steps);
res3  = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 1, 's', steps);
res4  = lzo_test (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps);
plot (res1(:,1), res1(:,2), 'r;m = 2, d = 6;', ...
      res2(:,1), res2(:,2), 'g;m = 3, d = 6;',...
      res3(:,1), res3(:,2), 'b;m = 4, d = 1;',...
      res4(:,1), res4(:,2), 'm;m = 4, d = 6;');
Tisean nl prediction.png

It seems that the last pair (m = 4, d = 6) is suitable. We will use it to determine the the best neighborhood to use when generating future points.

Code: Determining the best neighborhood size using lzo_gm 
gm = lzo_gm (amplitude(1:end-200), 'm', 4, 'd', 6, 's', steps, 'rhigh', 20);

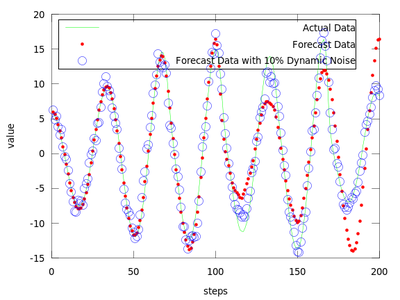
After analyzing gm it is easy to observe that the least error is for the first neighborhood size of gm which is equal to 0.49148. We will use it to produce the prediction vectors. Only the first 4800 datapoints from amplitude are used in order to compare the predicted values with the actual ones for the last 200 points.

Code: Creating forecast points 
steps          = 200;
forecast       = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148, 'l', steps);
forecast_noisy = lzo_run (amplitude(1:end-200), 'm', 4, 'd', 6, 'r', 0.49148,  ...
                          'dnoise', 10, 'l', steps);
plot (amplitude(end-199:end), 'g;Actual Data;', ...
      forecast, 'r.;Forecast Data;',...
      forecast_noisy, 'bo;Forecast Data with 10% Dynamic Noise;');
Tisean nl prediction 2.png

The difference between finding the proper r and not finding it can be very small.
The produced data is the best local zeroth order fit on the amplitude.dat for (m = 4, d = 6).

Nonlinear Noise Reduction

This tutorial show different methods of the 'Nonlinear Noise Reduction' section of the TISEAN documentation (located here). It shows the use of simple nonlinear noise reduction (function lazy) and locally projective nonlinear noise reduction (function ghkss). To start let's create noisy data to work with.

Code: Creating a noisy henon map 
hen       = henon (10000);
hen       = hen(:,1); # We only need the first column
hen_noisy = hen + std (hen) * 0.02 .* (-6 + sum (rand ([size(hen), 12]), 3));

This created a Henon map contaminated by 2% Gaussian noise à la TISEAN. In the tutorials and exercises on the TISEAN website this would be equivalent to calling makenoise -%2 on the Henon map.
Next we will reduce the noise using simple nonlinear noise reduction lazy.

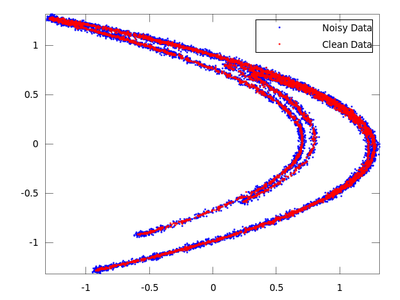
Code: Simple nonlinear noise reduction 
clean       = lazy (hen_noisy,7,-0.06,3);
# Create delay vectors for both the clean and noisy data
delay_clean = delay (clean);
delay_noisy = delay (hen_noisy);
# Plot both on one chart
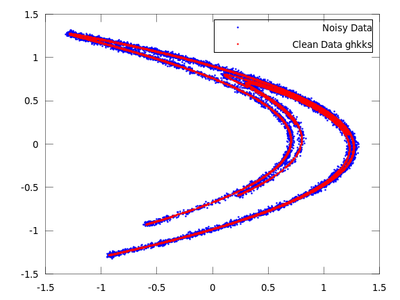
plot (delay_noisy(:,1), delay_noisy(:,2), 'b.;Noisy Data;','markersize',3,...
      delay_clean(:,1), delay_clean(:,2), 'r.;Clean Data;','markersize',3)
Tisean nl noisereduction.png

On the chart created the red dots represent cleaned up data. It is much closer to the original than the noisy blue set.
Now we will do the same with ghkss.

Code: Locally projective nonlinear noise reduction 
clean       = ghkss (hen,'m',7,'q',2,'r',0.05,'k',20,'i',2);

The rest of the code is the same as the code used in the lazy example.
Once both results are compared it is quite obvious that for this particular example ghkss is superior to lazy. The TISEAN documentation points out that this is not always the case.

Tisean nl noisereduction 2.png

Lyapunov Exponents

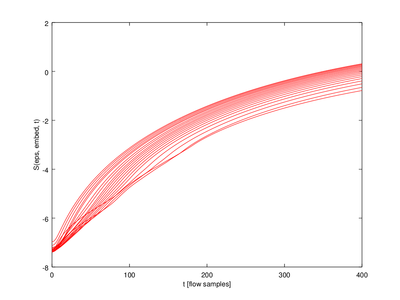
Here I will demonstrate how to use the function lyap_k. It estimates the maximal Lyapunov exponent from a time series (more information available from the TISEAN documentation located here). In this tutorial we will estimate the maximal Lyapunov exponent for various embedding dimensions and then plot them.

Code: Creating Lyapunov exponents 
# Create time series
in       = sin((1:2500).'./360) + cos((1:2500).'./180);
# Estimate Lyapunov exponents
mmax_val = 20
lyap_exp = lyap_k (in, 'mmin',2,'mmax',mmax_val,'d',6,'s',400,'t',500);

In this function the output (lyap_exp is a 5 x 20 struct array. We will only use one row for the plot.

Code: Plotting Lyapunov exponents 
cla reset
hold on
for j=2:mmax_val
  plot (lyap_exp(1,j-1).exp(:,1),lyap_exp(1,j-1).exp(:,2),'r');
endfor
xlabel ("t [flow samples]");
ylabel ("S(eps, embed, t)");
hold off
Lyap k.png

Dimensions and Entropies

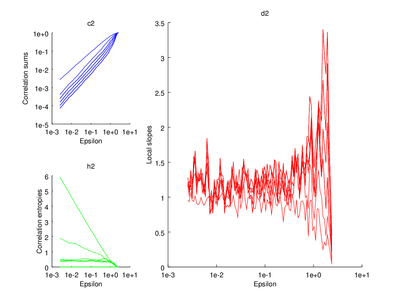
This section is discussed on the TISEAN documentation page. One of the functions discussed is d2. It is used to estimate the correlation sum, correlation dimension and correlation entropy of a time series. The time series used here will be the Henon map.

Code: Calculation correlation sum, dimension and entropy 
# Create maps
hen       = henon (10000);
# Calculate the correlation sum, dimension and entropy
vals = d2 (hen, 'd', 1, 'm', 5, 't',50);
# Plot correlation sum
subplot (2,3,1)
do_plot_corr  = @(x) loglog (x{1}(:,1),x{1}(:,2),'b');
hold on
arrayfun (do_plot_corr, {vals.c2});
hold off
xlabel ("Epsilon")
ylabel ("Correlation sums")
title ("c2");
# Plot correlation entropy
subplot (2,3,4)
do_plot_entrop  = @(x) semilogx (x{1}(:,1),x{1}(:,2),'g');
hold on
arrayfun (do_plot_entrop, {vals.h2});
hold off
xlabel ("Epsilon")
ylabel ("Correlation entropies");
title ("h2")
# Plot correlation dimension
subplot (2,3,[2 3 5 6])
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'r');
hold on
arrayfun (do_plot_slope, {vals.d2});
hold off
xlabel ("Epsilon")
ylabel ("Local slopes")
title ("d2");
D2 out.png

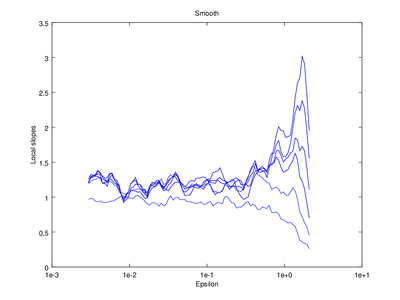
The output of d2 can be further processed using the following functions: av_d2, c2t, c2g. This tutorial will show how to use av_d2 which smooths the output of d2 (usually used to smooth the "d2" field of the output).

Code: Smooth output of d2 
# Smooth d2 output
figure 2
smooth = av_d2 (vals,'a',2);
# Plot the smoothed output
do_plot_slope = @(x) semilogx (x{1}(:,1),x{1}(:,2),'b');
hold on
arrayfun (do_plot_slope, {smooth.d2});
hold off
xlabel ("Epsilon")
ylabel ("Local slopes")
title ("Smooth");
Tisean av d2 out.png

Optionally the line "figure 2" can be omitted, which will cause the smoothed version to be superimposed on the "raw" version that came straight from d2.

External links

Retrieved from "https://wiki.octave.org/wiki/index.php?title=TISEAN_package&oldid=6550"