Control package: Difference between revisions
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
! Chapter !! Function !! Implemented !! File !! Status | ! Chapter !! Function !! Implemented !! File !! Status | ||
|- | |- | ||
| rowspan="11" | Basic Models || tf || style="background: | | rowspan="11" | Basic Models || tf || style="background: green;" | yes || @tf/tf.m || | ||
|- | |- | ||
| zpk || yes || zpk.m || | | zpk || style="background: green;" | yes || zpk.m || | ||
|- | |- | ||
| ss || yes || @ss/ss.m || | | ss || style="background: green;" | yes || @ss/ss.m || | ||
|- | |- | ||
| frd || yes || @frd/frd.m || | | frd || style="background: green;" | yes || @frd/frd.m || | ||
|- | |- | ||
| pid || no || || | | pid || style="background: red;" | no || || | ||
|- | |- | ||
| pidstd || no || || | | pidstd || style="background: red;" | no || || | ||
|- | |- | ||
| pid2 || no || || | | pid2 || style="background: red;" | no || || | ||
|- | |- | ||
| dss || yes || @lti/dss.m || | | dss || style="background: green;" | yes || @lti/dss.m || | ||
|- | |- | ||
| drss || no || || | | drss || style="background: red;" | no || || | ||
|- | |- | ||
| filt || yes || filt.m || | | filt || style="background: green;" | yes || filt.m || | ||
|- | |- | ||
| rss || no || || | | rss || style="background: red;" | no || || | ||
|- | |- | ||
|} | |} | ||
Revision as of 12:40, 23 September 2015
The control package is part of the Octave Forge project.
Function list
Linear System Representation
| Chapter | Function | Implemented | File | Status |
|---|---|---|---|---|
| Basic Models | tf | yes | @tf/tf.m | |
| zpk | yes | zpk.m | ||
| ss | yes | @ss/ss.m | ||
| frd | yes | @frd/frd.m | ||
| pid | no | |||
| pidstd | no | |||
| pid2 | no | |||
| dss | yes | @lti/dss.m | ||
| drss | no | |||
| filt | yes | filt.m | ||
| rss | no |
Model Interconnection
Model Transformation
Linear Analysis
Control Design
Matrix Computations
Some very basic examples
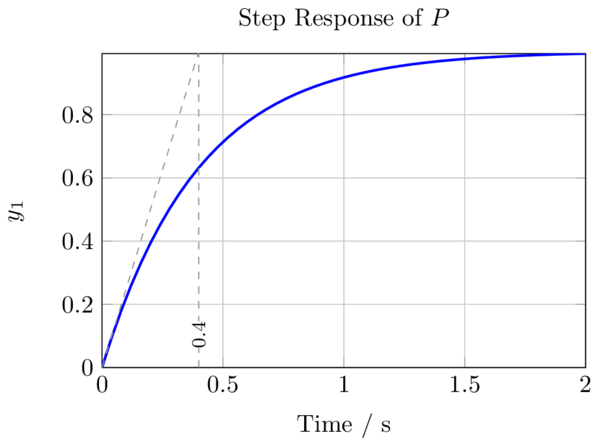
PT1/low-pass filter step response
| Code: Creating a transfer function and plotting its response |
T1=0.4; # time constant
P=tf([1], [T1 1]) # create transfer function model
step(P,2) # plot step response
#add some common markers like the tangent line at the origin, which crosses lim(n->inf) f(t) at t=T1
hold on
plot ([0 T1], [0 1],"g")
plot ([T1 T1], [0 1],"k")
plot ([0 T1], [1-1/e 1-1/e],"m")
hold off
|
Try also bode(P)! (a first order low-pass filter has -3db magnitude at f=1/T1)