Bim package: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
<math> -\mathrm{div}\ ( \varepsilon \nabla u(x, y) - \nabla \varphi(x,y)\ u(x, y) ) ) + u(x, y) = 1 </math> | <math> -\mathrm{div}\ ( \varepsilon \nabla u(x, y) - \nabla \varphi(x,y)\ u(x, y) ) ) + u(x, y) = 1 </math> | ||
p | |||
<math> \varphi(x, y) = x + y </math> | <math> \varphi(x, y) = x + y </math> | ||
Revision as of 16:30, 19 July 2012
This is a short example on how to use bim to solve a DAR problem.
The data for this example can be found in the doc directory inside the
bim installation directory.
We want to solve the equation
p
Create the mesh and precompute the mesh properties
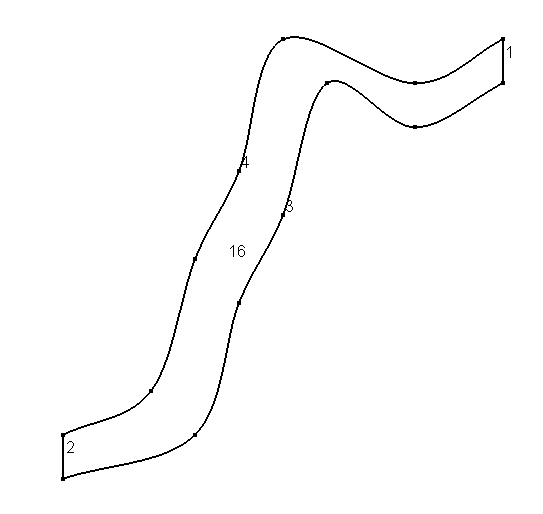
The geometry of the domain was created using gmsh and is stored in the file fiume.geo created with gmsh
[mesh] = msh2m_gmsh("fiume","scale",1,"clscale",.1);
[mesh] = bim2c_mesh_properties(mesh);
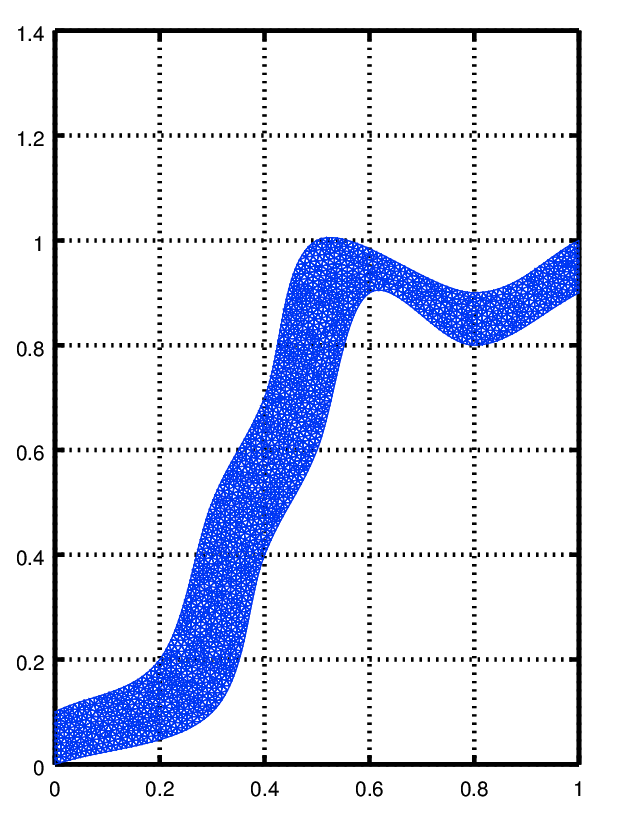
to see the mesh you can use functions from the [fpl] package
pdemesh (mesh.p, mesh.e, mesh.t) view (2)
Construct an initial guess
For a linear problem only the values at boundary nodes are actually relevant
xu = mesh.p(1,:).'; yu = mesh.p(2,:).'; nelems = columns(mesh.t); nnodes = columns(mesh.p); uin = 3*xu;
Set the coefficients for the problem:
epsilon = .1; alfa = ones(nelems,1); gamma = ones(nnodes,1); eta = epsilon*ones(nnodes,1); beta = xu+yu; delta = ones(nelems,1); zeta = ones(nnodes,1); f = ones(nelems,1); g = ones(nnodes,1);
Construct the discretized operators
AdvDiff = bim2a_advection_diffusion(mesh,alfa,gamma,eta,beta); Mass = bim2a_reaction(mesh,delta,zeta); b = bim2a_rhs(mesh,f,g); A = AdvDiff + Mass;
To Apply Boundary Conditions, partition LHS and RHS
The tags of the sides are assigned by gmsh
Dlist = bim2c_unknowns_on_side(mesh, [8 18]); ## DIRICHLET NODES LIST Nlist = bim2c_unknowns_on_side(mesh, [23 24]); ## NEUMANN NODES LIST Nlist = setdiff(Nlist,Dlist); Fn = zeros(length(Nlist),1); ## PRESCRIBED NEUMANN FLUXES Ilist = setdiff(1:length(uin),union(Dlist,Nlist)); ## INTERNAL NODES LIST
Add = A(Dlist,Dlist); Adn = A(Dlist,Nlist); ## shoud be all zeros hopefully!! Adi = A(Dlist,Ilist); And = A(Nlist,Dlist); ## shoud be all zeros hopefully!! Ann = A(Nlist,Nlist); Ani = A(Nlist,Ilist); Aid = A(Ilist,Dlist); Ain = A(Ilist,Nlist); Aii = A(Ilist,Ilist); bd = b(Dlist); bn = b(Nlist); bi = b(Ilist); ud = uin(Dlist); un = uin(Nlist); ui = uin(Ilist);
Solve for the displacements
temp = [Ann Ani ; Ain Aii ] \ [ Fn+bn-And*ud ; bi-Aid*ud]; un = temp(1:length(un)); ui = temp(length(un)+1:end); u(Dlist) = ud; u(Ilist) = ui; u(Nlist) = un;
Compute the fluxes through Dirichlet sides
Fd = Add * ud + Adi * ui + Adn*un - bd;
Compute the gradient of the solution
[gx, gy] = bim2c_pde_gradient(mesh,u);
Compute the internal Advection-Diffusion flux
[jxglob,jyglob] = bim2c_global_flux(mesh,u,alfa,gamma,eta,beta);
Save data for later visualization
fpl_dx_write_field("dxdata",mesh,[gx; gy]',"Gradient",1,2,1);
fpl_vtk_write_field ("vtkdata", mesh, {}, {[gx; gy]', "Gradient"}, 1);