Bim package: Difference between revisions
No edit summary |
|||
| Line 65: | Line 65: | ||
to see the mesh you can use functions from the [[fpl_package|fpl package]] | to see the mesh you can use functions from the [[fpl_package|fpl package]] | ||
< | {{Code|Plot mesh in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pdemesh (mesh.p, mesh.e, mesh.t) | pdemesh (mesh.p, mesh.e, mesh.t) | ||
view (2) | view (2) | ||
</ | </syntaxhighlight>}} | ||
[[File:fiume_msh.png]] | [[File:fiume_msh.png]] | ||
| Line 77: | Line 77: | ||
Get the node coordinates from the mesh structure | Get the node coordinates from the mesh structure | ||
< | {{Code|Get mesh coordinates in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
xu = mesh.p(1,:).'; | xu = mesh.p(1,:).'; | ||
yu = mesh.p(2,:).'; | yu = mesh.p(2,:).'; | ||
</ | </syntaxhighlight>}} | ||
Get the number of elements and nodes in the mesh | Get the number of elements and nodes in the mesh | ||
< | {{Code|Get number of elements in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
nelems = columns (mesh.t); | nelems = columns (mesh.t); | ||
nnodes = columns (mesh.p); | nnodes = columns (mesh.p); | ||
</ | </syntaxhighlight>}} | ||
<pre> | <pre> | ||
| Line 97: | Line 97: | ||
<b> Construct the discretized operators</b> | <b> Construct the discretized operators</b> | ||
< | {{Code|Discretized operators for the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
AdvDiff = bim2a_advection_diffusion (mesh, epsilon, 1, 1, phi); | AdvDiff = bim2a_advection_diffusion (mesh, epsilon, 1, 1, phi); | ||
Mass = bim2a_reaction (mesh, 1, 1); | Mass = bim2a_reaction (mesh, 1, 1); | ||
b = bim2a_rhs (mesh,f,g); | b = bim2a_rhs (mesh,f,g); | ||
A = AdvDiff + Mass; | A = AdvDiff + Mass; | ||
</ | </syntaxhighlight>}} | ||
<b> To Apply Boundary Conditions, partition LHS and RHS</b> | <b> To Apply Boundary Conditions, partition LHS and RHS</b> | ||
| Line 109: | Line 109: | ||
and <math> \Gamma_D </math> be the rest of the boundary | and <math> \Gamma_D </math> be the rest of the boundary | ||
< | {{Code|Boundary conditions for the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
GammaD = bim2c_unknowns_on_side (mesh, [1 2]); ## DIRICHLET NODES LIST | GammaD = bim2c_unknowns_on_side (mesh, [1 2]); ## DIRICHLET NODES LIST | ||
GammaN = bim2c_unknowns_on_side (mesh, [3 4]); ## NEUMANN NODES LIST | GammaN = bim2c_unknowns_on_side (mesh, [3 4]); ## NEUMANN NODES LIST | ||
| Line 117: | Line 117: | ||
ud = 3*xu; ## DIRICHLET DATUM | ud = 3*xu; ## DIRICHLET DATUM | ||
Omega = setdiff (1:nnodes, union (GammaD, GammaN)); ## INTERIOR NODES LIST | Omega = setdiff (1:nnodes, union (GammaD, GammaN)); ## INTERIOR NODES LIST | ||
Add = A(GammaD, GammaD); | Add = A(GammaD, GammaD); | ||
Adn = A(GammaD, GammaN); ## shoud be all zeros hopefully!! | Adn = A(GammaD, GammaN); ## shoud be all zeros hopefully!! | ||
| Line 136: | Line 133: | ||
bn = b(GammaN); | bn = b(GammaN); | ||
bi = b(Omega); | bi = b(Omega); | ||
</ | </syntaxhighlight>}} | ||
<B> Solve for the displacements</B> | <B> Solve for the displacements</B> | ||
< | {{Code|Displacement in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
temp = [Ann Ani ; Ain Aii ] \ [ jn+bn-And*ud(GammaD) ; bi-Aid*ud(GammaD)]; | temp = [Ann Ani ; Ain Aii ] \ [ jn+bn-And*ud(GammaD) ; bi-Aid*ud(GammaD)]; | ||
u = ud; | u = ud; | ||
u(GammaN) = temp(1:numel (GammaN)); | u(GammaN) = temp(1:numel (GammaN)); | ||
u(Omega) = temp(length(GammaN)+1:end); | u(Omega) = temp(length(GammaN)+1:end); | ||
</ | </syntaxhighlight>}} | ||
<b> Compute the fluxes through Dirichlet sides</b><br> | <b> Compute the fluxes through Dirichlet sides</b><br> | ||
< | {{Code|Fluxes at sides in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
jd = [Add Adi Adn] * u([GammaD; Omega; GammaN]) - bd; | jd = [Add Adi Adn] * u([GammaD; Omega; GammaN]) - bd; | ||
</ | </syntaxhighlight>}} | ||
<B> Compute the gradient of the solution </B> | <B> Compute the gradient of the solution </B> | ||
< | {{Code|Gradient of solution in the 2D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
[gx, gy] = bim2c_pde_gradient (mesh, u); | [gx, gy] = bim2c_pde_gradient (mesh, u); | ||
</ | </syntaxhighlight>}} | ||
<B> Compute the internal Advection-Diffusion flux</B> | <B> Compute the internal Advection-Diffusion flux</B> | ||
| Line 203: | Line 201: | ||
<math> u = \exp (- \left(\frac{x-.2}{.2}\right)^2 - \left(\frac{y-.2}{.2}\right)^2 - \left(\frac{z-.2}{.2}\right)^2)</math> | <math> u = \exp (- \left(\frac{x-.2}{.2}\right)^2 - \left(\frac{y-.2}{.2}\right)^2 - \left(\frac{z-.2}{.2}\right)^2)</math> | ||
< | {{Code|Define the 3D problem|<syntaxhighlight lang="octave" style="font-size:13px"> | ||
pkg load bim | pkg load bim | ||
| Line 238: | Line 236: | ||
fpl_vtk_write_field (name, msh, {U(ii,:)', 'u'}, {}, 1); | fpl_vtk_write_field (name, msh, {U(ii,:)', 'u'}, {}, 1); | ||
endfor | endfor | ||
</ | </syntaxhighlight>}} | ||
[http://youtu.be/2E6Z_AcV8CQ This is a video] showing the .3 isosurface of the solution. | [http://youtu.be/2E6Z_AcV8CQ This is a video] showing the .3 isosurface of the solution. | ||
Revision as of 15:40, 20 July 2012
Package for solving Diffusion Advection Reaction (DAR) Partial Differential Equations based on the Finite Volume Scharfetter-Gummel (FVSG) method a.k.a Box Integration Method (BIM).
Tutorials
2D Diffusion Advection Reaction example
This is a short example on how to use bim to solve a 2D Diffusion Advection Reaction problem. The coplete code for this example can is on Agora at this link.
We want to solve the equation
with mixed Dirichlet / Neumann boundary conditions
Create the mesh and precompute the mesh properties
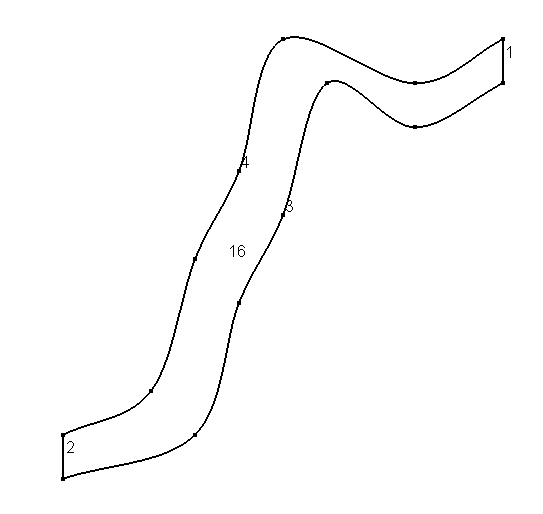
To define the geometry of the domain we can use gmsh.
the following gmsh input
Point (1) = {0, 0, 0, 0.1};
Point (2) = {1, 1, 0, 0.1};
Point (3) = {1, 0.9, 0, 0.1};
Point (4) = {0, 0.1, 0, 0.1};
Point (5) = {0.3,0.1,-0,0.1};
Point (6) = {0.4,0.4,-0,0.1};
Point (7) = {0.5,0.6,0,0.1};
Point (8) = {0.6,0.9,0,0.1};
Point (9) = {0.8,0.8,0,0.1};
Point (10) = {0.2,0.2,-0,0.1};
Point (11) = {0.3,0.5,0,0.1};
Point (12) = {0.4,0.7,0,0.1};
Point (13) = {0.5,1,0,0.1};
Point (14) = {0.8,0.9,0,0.1};
Line (1) = {3, 2};
Line (2) = {4, 1};
CatmullRom(3) = {1,5,6,7,8,9,3};
CatmullRom(4) = {4,10,11,12,13,14,2};
Line Loop(15) = {3,1,-4,2};
Plane Surface(16) = {15};
will produce the geometry below
we need to load the mesh into Octave and precompute mesh properties check out the tutorial for the msh package for info on the mesh structure
| Code: Meshing the 2D problem |
[mesh] = msh2m_gmsh ("fiume","scale",1,"clscale",.1);
[mesh] = bim2c_mesh_properties (mesh);
|
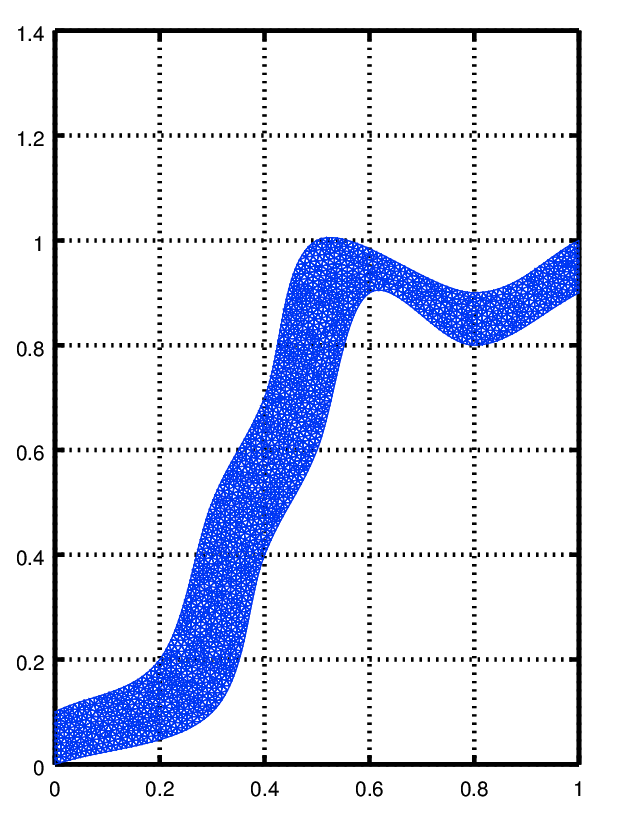
to see the mesh you can use functions from the fpl package
| Code: Plot mesh in the 2D problem |
pdemesh (mesh.p, mesh.e, mesh.t)
view (2)
|
Set the coefficients for the problem:
Get the node coordinates from the mesh structure
| Code: Get mesh coordinates in the 2D problem |
xu = mesh.p(1,:).';
yu = mesh.p(2,:).';
|
Get the number of elements and nodes in the mesh
| Code: Get number of elements in the 2D problem |
nelems = columns (mesh.t);
nnodes = columns (mesh.p);
|
epsilon = .1; phi = xu + yu;
Construct the discretized operators
| Code: Discretized operators for the 2D problem |
AdvDiff = bim2a_advection_diffusion (mesh, epsilon, 1, 1, phi);
Mass = bim2a_reaction (mesh, 1, 1);
b = bim2a_rhs (mesh,f,g);
A = AdvDiff + Mass;
|
To Apply Boundary Conditions, partition LHS and RHS
The tags of the sides are assigned by gmsh we let be composed by sides 1 and 2 and be the rest of the boundary
| Code: Boundary conditions for the 2D problem |
GammaD = bim2c_unknowns_on_side (mesh, [1 2]); ## DIRICHLET NODES LIST
GammaN = bim2c_unknowns_on_side (mesh, [3 4]); ## NEUMANN NODES LIST
GammaN = setdiff (GammaN, GammaD);
jn = zeros (length (GammaN),1); ## PRESCRIBED NEUMANN FLUXES
ud = 3*xu; ## DIRICHLET DATUM
Omega = setdiff (1:nnodes, union (GammaD, GammaN)); ## INTERIOR NODES LIST
Add = A(GammaD, GammaD);
Adn = A(GammaD, GammaN); ## shoud be all zeros hopefully!!
Adi = A(GammaD, Omega);
And = A(GammaN, GammaD); ## shoud be all zeros hopefully!!
Ann = A(GammaN, GammaN);
Ani = A(GammaN, Omega);
Aid = A(Omega, GammaD);
Ain = A(Omega, GammaN);
Aii = A(Omega, Omega);
bd = b(GammaD);
bn = b(GammaN);
bi = b(Omega);
|
Solve for the displacements
| Code: Displacement in the 2D problem |
temp = [Ann Ani ; Ain Aii ] \ [ jn+bn-And*ud(GammaD) ; bi-Aid*ud(GammaD)];
u = ud;
u(GammaN) = temp(1:numel (GammaN));
u(Omega) = temp(length(GammaN)+1:end);
|
Compute the fluxes through Dirichlet sides
| Code: Fluxes at sides in the 2D problem |
jd = [Add Adi Adn] * u([GammaD; Omega; GammaN]) - bd;
|
Compute the gradient of the solution
| Code: Gradient of solution in the 2D problem |
[gx, gy] = bim2c_pde_gradient (mesh, u);
|
Compute the internal Advection-Diffusion flux
[jxglob, jyglob] = bim2c_global_flux (mesh, u, epsilon*ones(nelems, 1), ones(nnodes, 1), ones(nnodes, 1), phi);
Export data to VTK format
The resut can be exported to vtk format to visualize with [[1]] or [[2]]
fpl_vtk_write_field ("vtkdata", mesh, {u, "Solution"}, {[gx; gy]', "Gradient"}, 1);
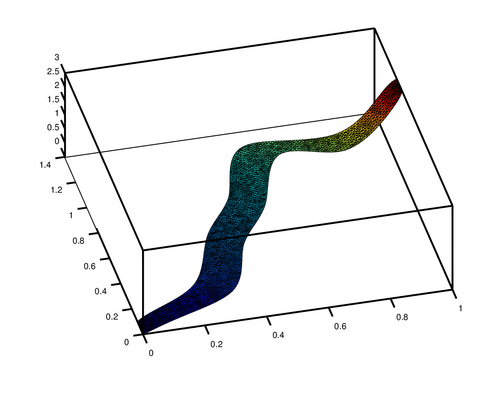
you can also plot your data directly in Octave using pdesurf
pdesurf (mesh.p, mesh.t, u)
it will look like this
3D Time dependent problem
Here is an example of a 3D time-dependent Advection-Diffusion equation that uses lsode for time-stepping.
The equation being solved is
The initial condition is
| Code: Define the 3D problem |
pkg load bim
x = linspace (0, 1, 40);
y = z = linspace (0, 1, 20);
msh = bim3c_mesh_properties (msh3m_structured_mesh (x, y, z, 1, 1:6));
nn = columns (msh.p);
ne = columns (msh.t);
x = msh.p(1, :).';
y = msh.p(2, :).';
z = msh.p(3, :).';
x0 = .2; sx = .1;
y0 = .2; sy = .1;
z0 = .8; sz = .1;
u = exp (- ((x-x0)/(2*sx)) .^2 - ((y-y0)/(2*sy)) .^2 - ((z-z0)/(2*sz)) .^2);
A = bim3a_advection_diffusion (msh, .01*ones(ne, 1), 100*(x+y-z));
M = bim3a_reaction (msh, 1, 1);
function du = f (u, t, A, M)
du = - M \ (A * u);
endfunction
time = linspace (0, 1, 30);
lsode_options ("integration method", "adams");
U = lsode (@(u, t) f(u, t, A, M), u, time);
for ii = 1:1:numel (time)
name = sprintf ("u_%3.3d", ii);
delete ([name ".vtu"]);
fpl_vtk_write_field (name, msh, {U(ii,:)', 'u'}, {}, 1);
endfor
|
This is a video showing the .3 isosurface of the solution.





![{\displaystyle {\frac {\partial u}{\partial t}}-\mathrm {div} \left(.01\nabla u-u\nabla \varphi \right)=0\qquad {\mbox{ in }}\Omega \times [0,T]=[0,1]^{3}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3733151631f4fa649cf6dc34c0433c240f6a9c08)


